上海哪里有AMC12培训班？AMC12竞赛有哪些知识点？

AMC8、AMC10、AMC12竞赛里，AMC12的难度是最大的，考察的知识点也是最多的，需要花费的备考时间也相对来说是最长的，一文详解丨AMC12竞赛知识点/难题分布/高分备考方案！

代数：加减乘除四种基本运算，表达式（例如：线性，二次，多项式，指数表达式），方程（例如：线性，二次，多项式，指数方程），函数（例如：线性，二次，多项式，指数函数），数列（例如：等差数列，等比数列），对数，复数，三角函数。

几何：基础欧式平面几何（例如：勾股定理，全等三角形，相似三角形，特殊形状的四边形，圆），立体几何（例如：体积和表面积公式，空间想象力），解析几何（例如：直线和圆的方程），正弦定理，余弦定理，四点共圆。

计数和概率：计数的加法原理，计数的乘法原理，排列，组合，古典概率模型，条件概率，基础统计（例如：平均值，中位数，众数）。

数论：质数与合数，分解质因数，进制，整除，模运算。

应用问题：比例分析，单位转换，分数和百分数。

AMC12题目难度分布

 

 

1-10题为基础题，大部分学生都能完成；

 

11-20题比较有深度，难度增大，且题目考查形式较为灵活；

 

21-23题综合考察知识点内容，题目的深度和广度有所增加；

 

24-25题，难度很大，对考生数学思维要求高，综合性考察重难点知识内容；

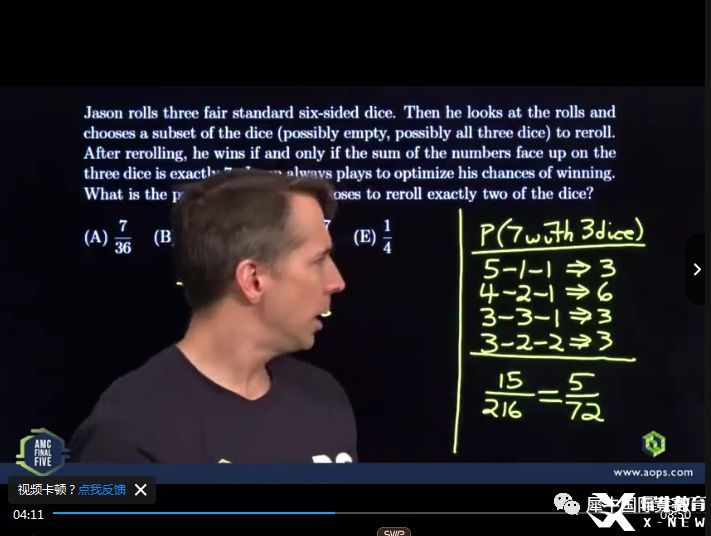
有需要AMC12难题解析视频的同学

请找在线客服领取

区分AMC12考点所涵盖的知识阶段

小学与小奥:运算与巧算、基本几何图形、比例与比例应用、简单立体几何计算、行程问题与具体复杂应用、计数、等差与等比

初中:多项运算变形、整体方程与不合理方程、一/二次函数与数形结合、三角形与圆形在平面几何中的相关性质定理及相关问题、统计相关问题

高中:韦达定理与高次方程，指对数运算与变形、数列与计算、三角函数运算与恒等变形与应用、正余弦定理、复数计算与应用、几何分析、排列组合与概率模型、复杂构造函数方程问题

确定考试目标，制定相应的策略

AMC12入门的“获奖”门槛相对较低，但想进入前5%HR和前1%DHR的难度相对较高。备考AMC12前应该结合自身学习情况、投入时间和精力、想要达到的目标，来考虑适合自己的备考方案。

注意训练，正视做题

很多准备AMC12的学生同时有很多学习任务。训练题对很多学生来说比较枯燥，很难坚持。对于想要影响奖项的学生来说，要非常重视完成训练，有目的地刻意练习题目。没有基本的训练，很容易想不出如何处理或者知道几个模糊的解题方向，但是浪费了很多时间，所以刷题一定是必须的。