AMC10晋级率怎么样？晋级AIME考察知识点及培训课程介绍！

AMC10晋级率是多少？晋级率每年的变化是怎样的呢？对于AMC10考试中想要晋级AIME的学生，需要做好哪些准备？AMC10及AIME考试知识点对比分析，考试时间紧张，做好准备很重要。从AMC10到AIME，考试的难度以及知识点都会增加，并且考试时间相近，想要冲刺高分，提前准备很有必要，AMC10及AIME竞赛培训辅导课程安排，了解一下：

AMC10晋级率是多少？

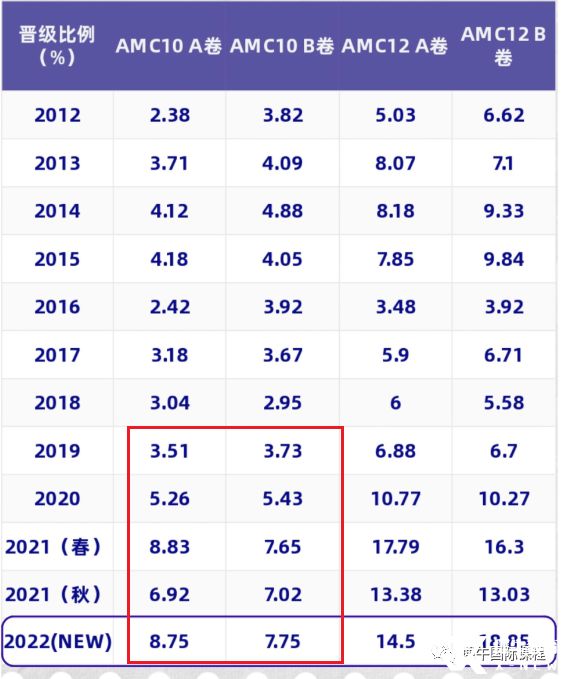
AMC10 A卷晋级AIME的比例一直在相对稳定的范围内波动。2012年的晋级率最低，为2.38%，而2015年达到最高值，为4.18%。然而，在2020年至2022年秋季的三场考试中，晋级率出现了明显的增长，分别为5.26%、8.83%（历年最高）和6.92%。

AMC10 B卷晋级AIME的比例也出现了轻微变化。2018年的晋级率最低，为2.95%，而2014年达到最高值，为4.88%。然而，在2020年至2021年秋季的三场考试中，AMC10 B卷的晋级率显著增加，分别为5.43%、7.65%（历年最高）和7.02%。

由此可见，近三年为AIME考生的黄金时代，希望所有考生不要放弃AIME的冲刺机会。

AMC10对比AIME

AMC10竞赛是选择题，AIME竞赛是填空题，考察形式变化明显，学生不能使用猜测法等，需要有扎实的学术功底，因此AMC10阶段，学生们应该夯实基础，掌握解题方法。

AIME竞赛中的知识点更难更深，与AMC12相似，并且在几何、数论、组合模块多了部分的知识点，错综复杂，尤其是最后的5题，难度提升明显，针对学霸设置，因此，巩固基础是核心。

AIME题目的最大特点是灵活性、综合性和多样性。考生需要具备强大的思维发散能力，不应受限于刻板的公式和套路，而是要真正理解、思考和联想，去揭示隐藏在众多表面线索背后的本质。

灵活性：AIME中许多题目的考察重点并不是固定的知识点（性质或公式），而是背后的一些数学思想。

举例来说，在代数部分，无论是涉及对数、三角还是复数的题目，都可能考察一些代数变形的思想和技巧，如整体代换、因式分解、递推方法、对称式和轮换式、自相似以及赋予代数式几何含义等。这些技巧非常灵活，不能仅靠死记硬背的公式来套用，而需要考生在看到题目时进行思考、分析和尝试，确定最合适的方法，并随后进行求解。

综合性：AIME的许多题目常涉及多个模块的知识点，即跨领域的题目。

例如，一道涉及三角函数的题目可能需要运用复数和多项式技巧以及几何性质；一道几何题可能会使用复数和坐标系方法；一道代数题若有多个整数条件，可能与数论密切相关；一道概率计算题最终可能转化为递推数列求解或多重数列求和问题。这种交叉领域的考察要求考生具备广泛的数学知识，并能灵活应用于不同的情境中。

多样性：AIME的题目通常有多个切入点，并可以采用多种解法。

举例来说，一道组合题可以通过分类讨论和枚举解决，也可以利用递推进行计算，还可以运用一一对应的方法一步解决。一道几何题可以通过勾股定理和相似性解决，也可以使用三角函数进行暴力计算，或者采用建立坐标系的方法求解。因此，在解答AIME题目时，具备多种解题技巧的学生更容易找到最合适的方法，从而提高正确率。

AMC10及AIME备考课程

AIME竞赛的考试时间为2月；

想要冲刺AIME高分，等到AMC10/12成绩公布后，再去备考，时间会非常的紧张，有效的学习时间不足2个月，因此做好AIME冲刺计划同样重要。

对于计划参加今年AMC竞赛培训的同学，犀牛针对不同的学员目前开设了AMC全程班，冲刺班，模考点评班等多种班型，暑期培训辅导班火爆招生中

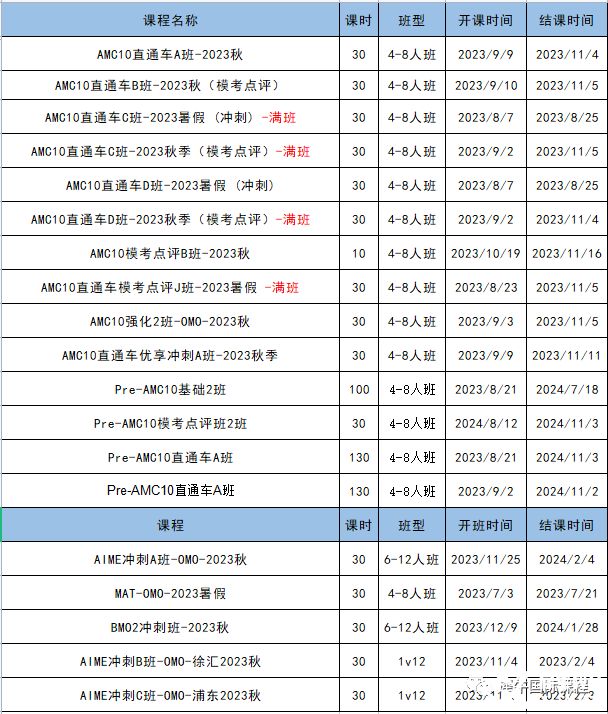
AMC竞赛培训课表（部分）

AMC暑期班不断满班中……

学生可在犀牛专项测试之后，选择合适的课程学习，也可以进行自组班学习，更多详情欢迎扫描下方二维码咨询。

 

AMC数学竞赛培训课程：咨询网站客服了解

犀牛AMC线上课程展示

犀牛教育AIME 课程大纲

 

Lecture1：三角函数与解三角形

Lecture2：方程：方程组（含解析几何）与高次方程

Lecture3：方程：齐次方程、不定方程、韦达定理

Lecture4：双圆与多圆问题

Lecture5：数列专题--一阶与二阶差分数列

Lecture6：数列与概率--递归与递推数列

Lecture7：解析几何专题：数形结合思想

Lecture8：数列与数论综合题

Lecture9：概率：复杂的离散型概率（结合分类讨论）

Lecture10：抽象函数与迭代以及六大函数性质应用

Lecture11~13：数学思想与数学方法、12个AIME专题（共10种）

Lecture14~15：模考与题目综合训练

 

 

AIME培训辅导课程：咨询网站客服了解