2023年AMC10报名马上截止，这20个备考公式不能错过！

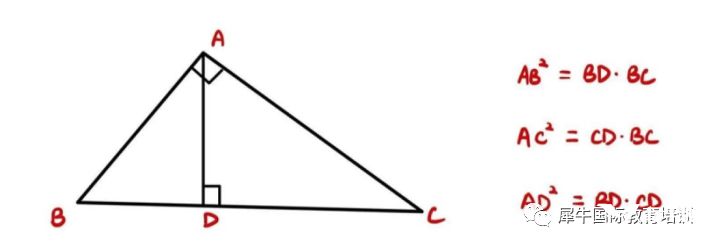
3、角平分线定理

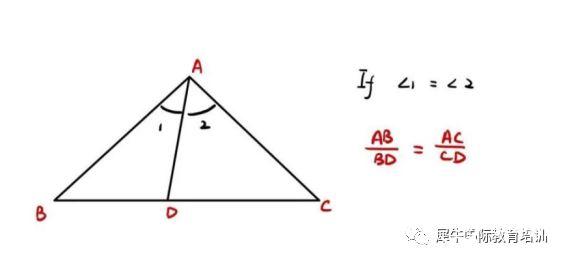
4、利用正余弦三角形面积

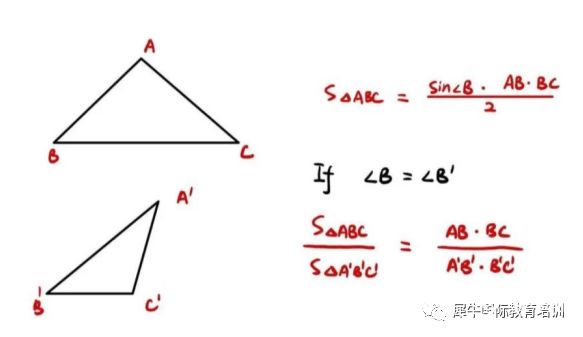
5、斯图尔特定理

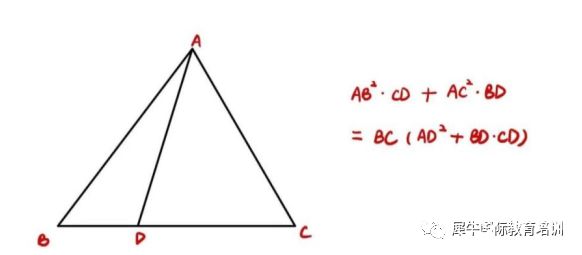
1、韦达定理

2、算术平均-几何平均不等式

3、二项式定理

4、合分比定理

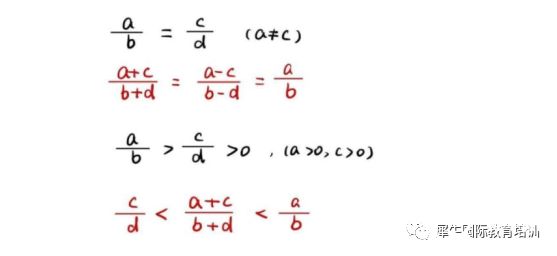
5、余数定理

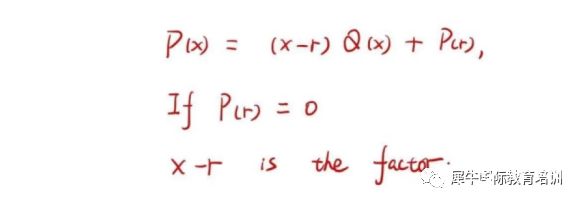
1、孙子定理

2、费马小定理

假如 p是质数，若p不能整除a，则 a^(p-1) ≡1 (mod p) ，

若p能整除a，则a^(p-1) =0 (mod p) 。

若p是质数，且a,p 互质，那么a的(p-1)次方除以p的余数恒

等于1。

3、威尔逊定理

若p为质数，则p可整除(p-1)!+1

4、欧几里得算法

两个数的最大公约数是指两个数的共有约数中的最大一个，例

如,(6,9)的最大公约数为3;(10,15)的最大公约数为5;(252,105)的最大公约数为21；

欧几里得算法可以高效地求解两个正整数(a,b)的最大公约数

(greatest common divisor, GCD).该算法基于如下定理:对于

正整数(a,b)，其最大公约数等于(b,c)的最大公约数，其中，

c = a % b;基于上述思想，可以将该算法写成递归的形式：

保证a>b；

当 a %b==0 成立时，表明b为a的约数，且b为(a,b)二者的最大公约数，所以返回b；

若 a % b!= 0 成立时，重复步骤2，寻找(b, a % b) 的最大公约数。

5、立方和公式

立方和的公式是:a³+b³=(a+b)(a²-ab+b²)

6、欧拉定理

1、互补计数

互补计数，顾名思义就是计算所求集合中补集的元素个数。典型的例子是找出“至少有n个”的互补情况，也就是“至多有

n-1”。

结合题目中出现的"至多"、“至少”这样的关键词，利用互补

的思想，可以使一些计数和概率计算变得更简洁有效。

2、容斥原理

两个集合的容斥关系公式：AUB=A+B-ANB(N为重合的部分)

三个集合的容斥关系公式：AUBUC=A+B+C-ANB-BNC-CN

A+ANBNC。

三集合容斥问题的核心公式如下:

标准型：

|AUBUC|=|A|+|B|+|C|-|ANB|-|BNC|-|CNA|+|ANBNC |。

非标准型：|AUBUC|=|A|+|B|+|C|-只满足两个条件

的-2x三个都满足的。

列方程组：|AUBUC|=只满足一个条件的+只满足两个条件

的+三个都满足的。

|A|+|B|+|C|=只满足一个条件的+2x只满足两个条件的

+3x三个都满足的，对于以上三组公式的理解，可以通过想象

三个圆两两相交的重叠情况来加深。

3、隔板法

隔板法就是在n个元素间的(n-1)个空中插入若干个(b)个

板，可以把n个元素分成(b+1)组的方法。

应用隔板法必须满足三个条件:

❶、这n个元素必须互不相异

❷、所分成的每一组至少分得一个元素

❸、分成的组别彼此相异

4、抽屉原理

原理1：把n+1个元素分成n类,不管怎么分,则一定有一类中有2个或2个以上的元素；

原理2: 把m个元素任意放入n(n<m=个集合,则一定有一个集合呈至少要有k个元素；

原理3：把无穷多个元素放入有限个集合里,则一定有一个集合里含有无穷多个元素

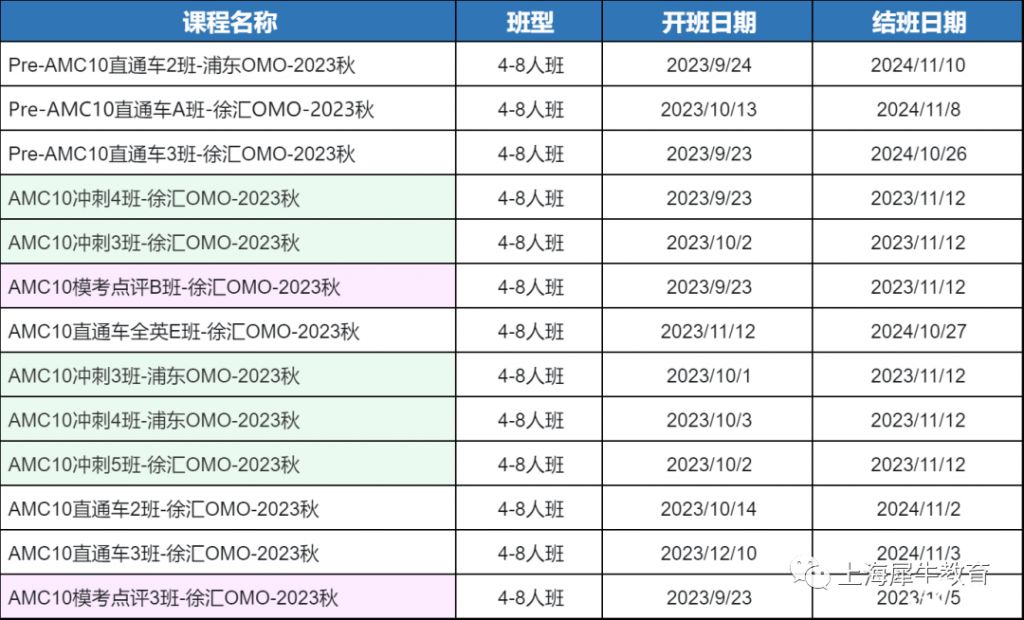
AMC10/12今年11月开考，现在进入备赛冲刺阶段，想要拿奖，晋级AIME的同学们，建议在犀牛教育AMC冲奖班进行提升

课程类型：一对一辅导/4-8人小班课

授课模式：线上/线下同步授课，有课程回放录像可供复习

授课语言：中/英双语教学

校区分布：北京、上海、广州、深圳、杭州、苏州、南京、无锡、青岛、合肥、武汉、济南、成都等地均有校区。