1月USACO计算机竞赛'银牌'解题分析（完整版可领取）

发布时间：2024-02-02 09:34:32

编辑：Lisa来源：未知浏览：次

USACO竞赛1月月赛真题解析有吗？USACO竞赛怎么备考？USACO竞赛真题解析来啦，参加了2024年1月的USACO月赛的同学，快来对答案！
USACO计算机竞赛的1月月赛悄然落幕！参赛的同学们觉得题目难吗？给大家整理了此次银牌考试试题+题解+代码，考完的同学们可以来参考交流一下。想要领取此次真题全部解析和有备考计划的同学，可以在线领取

- X-NEW-

USACO 2024年1月银牌第一题

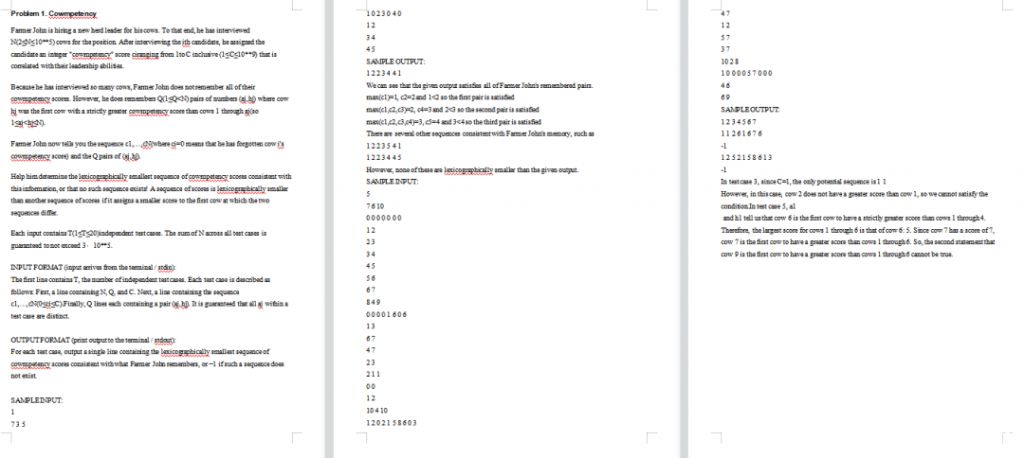
题解分析：

有q对(x,y)的输入，每对表示前1~x个数右边第一个比它们大的数必须在下标为y的位置，这句话还有一个隐藏含义就是第x+1到第y-1个数必须比前1~x个数的最大值要小，即第y个数比前y-1个数都要大(代码中称为前缀最大值)。

用一个前缀和数组pre_max[i]表示前i个数中的最大值，则a[y]至少为pre_max[y-1]+1。

现在从左往右遍历a[N]，分类讨论每一个a[i]的情况：

1.a[i]==0且位置i是前缀最大值，令a[i]=pre_max[y-1]+1

2.a[i]==0 且不是前缀最大值，根据贪心思路令a[i]=1 （字典序最小）

3.a[i]不为0，是第x+1到第y-1个数的其中一个，但是比前x个数要大，破坏了前缀最大值的要求，此时需要把之前的某个能改的值提高为a[i]

对全部a[N]修改完毕后，再重新for循环扫描一遍看看新的a[N]有没有冲突，有冲突输出-1

注意事项：这题有T个测试，每个输出最后不能带空格

代码：

//Q x y 的限制等价于是y是前缀最大值，x+1~y-1内的元素不能是前缀最大值
//贪心，对于不是前缀最大值的填1，是前缀最大值的填前缀max再+1
//注意有时候需要反悔，由于当前值是前缀最大值但是题目要求它不能是，只能把之前的值改大
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int a[N],sum[N],f[N],b[N];
int main(){
   int T;
   cin>>T;
   while (T--){
       int n,m,c;
       cin>>n>>m>>c;
       for (int i=1;i<=n;i++) cin>>a[i];
       for (int i=1;i<=m;i++){
           int x,y;
           cin>>x>>y;
           f[y]=1; //f代表是前缀最大值
           sum[x+1]++; sum[y]--; //前缀和看哪些不是前缀最大值
       }
       for (int i=1;i<=n;i++) sum[i]+=sum[i-1];
       int mx=1;
       int pre=0;
       for (int i=1;i<=n;i++){
           if (a[i]==0){
               if (f[i]) a[i]=mx+1; //前缀max
               else a[i]=1; //不是前缀max
               if (sum[i]==0) pre=i; //记录能修改的位置
           }
           if (sum[i]>0&&a[i]>mx){
               a[pre]=a[i];
           }
           mx=max(mx,a[i]); //最大值
       }
       bool tt=1;
       for (int i=1;i<=n;i++) { //判断是否合法
          b[i]=max(b[i-1],a[i]);
          if (a[i]>c) tt=0;
          if (b[i-1]<a[i]&&sum[i]>0) tt=0;
          if (b[i-1]>=a[i]&&f[i]) tt=0;
        }
        if (!tt){
           cout<<-1<<endl;
        } else {
           for (int i=1;i<n;i++) cout<<a[i]<<" ";
           cout<<a[n]<<endl;
        }
       for (int i=1;i<=n+10;i++) sum[i]=0,f[i]=0;
   }
   return 0;
}

USACO 2024年1月银牌第二题

题解分析：

以房间1为根节点的树。每次traversal相当于从根出发，沿着父子关系一直走，一个traversal的终点一定是一个叶节点，因此最小的traversal数必定为叶节点数量，可以用dfs得到，假设这个数量是k。

可以用树上DP来记录每个节点的子树拥有的叶节点数量，状态转移方程为dp[fa] += dp[child],则dp[1]就是整棵树拥有的叶节点数量

此时来看题目对potion的描述，每次traversal会在一个节点生成一个potion，下一次traversal前消失，而我们只会有k个(即dp[1]个)traversal。

因此实际上只需要考虑前k个potion。而由于potion是依靠traversal获取的，因此potion和traversal,也就是叶节点，是一对一绑定的。假设我们目前在某个节点p，从点p出发获得的potion数量不会超过点p的子树拥有的叶节点数量。我们再用一个树上DP，potion[p]表示点p的子树拥有的potion数量，状态转移方程为potion[fa] += potion[child]。统计完毕后再令potion[p] = min(potion[p], dp[p])。

最终potion[1]就是本题答案。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
vector<int> G[N];
int a[N],f[N],dp[N];
void dfs(int x,int y){ //dp[x]代表每个点往下叶子个数
   for (auto v:G[x])
      if (v!=y){
          dfs(v,x);
          dp[x]+=dp[v];
      }
   if (!dp[x]) dp[x]=1;
}
void dfs2(int x,int y){//f[x]代表每个点往下叶子个数和到达点个数的min
   int ans=0;
   for (auto v:G[x])
      if (v!=y){
          dfs2(v,x);
          f[x]+=f[v];
      }
   f[x]=min(f[x],dp[x]);
}
int main(){
   int n;
    cin>>n;
    for (int i=1;i<=n;i++) cin>>a[i];
    for (int i=1;i<n;i++){
       int x,y;
       cin>>x>>y;
       G[x].push_back(y);
       G[y].push_back(x);
    }
    dfs(1,0);
    for (int i=1;i<=dp[1];i++) f[a[i]]++; //只有前叶子个数个是有用的
    dfs2(1,0);
   cout<<f[1]<<endl;
   return 0;
}

USACO 2024年1月银牌第三题

题解分析：

抽屉原理+同余性质

题目等价于N个数除以L最多只有3个不同的余数，根据抽屉原理，任意选择4个不同的数，必定至少有两个数a[i]和a[j]除以L的余数相同(即模L同余)。由同余的基本性质可知abs(a[i]-a[j])必定能被L整除。

因此本题只需要从a[N]中任选4个不同的数，枚举它们的两两差值(一共有 = 6 种)，对这6个数，枚举它们的所有因子fac，进行检验（看看a[1]到a[N]除以fac是不是最多只有3个余数），符合要求则令ans+=fac。

代码：

//抽屉原理 4个数里一定有一个相同种类的 L一定是a[i]-a[j]的因数
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int a[N],f[N],n;
int sum=0;
void check(int x){ //检验x是否合法
   vector<int> v;
   for (int i=1;i<=n;i++){
       int t=a[i]%x;
       bool pp=0;
       for (auto p:v){
           if (p==t) pp=1;
       }
       if (!pp) v.push_back(t);
       if (v.size()>3) break;
   }
   if (v.size()<=3) sum+=x;
}
signed main(){
    cin>>n;
    for (int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1);
    n=unique(a+1,a+n+1)-a-1;
   //排序去重
    if (n<=3){
       //3个数任意答案都合法
       int x=a[1]/4;
       cout<<(x+1)*x/2<<endl;
       return 0;
    }
    int ans=1e10,now=1;
    for (int i=1;i<=n-3;i++) {
       if (a[i+3]-a[i]<ans){
           now=i;
           ans=a[i+3]-a[i];
       }
    }
   //找到最小差值随便找其实也是对的
    vector<int> v;
    map<int,bool> M;
   v.push_back(a[now+1]-a[now]);
   v.push_back(a[now+2]-a[now]);
   v.push_back(a[now+3]-a[now]);
   v.push_back(a[now+2]-a[now+1]);
   v.push_back(a[now+3]-a[now+1]);
   v.push_back(a[now+3]-a[now+2]);
   for (auto vv:v){ //标记因数
       if (vv>0){
           for (int j=1;j*j<=vv;j++)
           if (vv%j==0)
           {
               M[j]=1;
               M[vv/j]=1;
           }
       }
   }
   for (auto v:M){
       if (v.first*4<=a[1]){
           check(v.first);
       }
   }
   cout<<sum<<endl;
   return 0;
}

USACO备考:

USACO的参赛选手必须依次通过青铜、白银、黄金，直至最高级铂金，不可跳级，但是实力足够，可以连续晋级。铂金级选手如果有足够的精力，可以继续参赛打排名，争取拿到美国国家集训队（Camp）的Offer。因此在备赛过程中，可以提前准备，不必等通过一个级别后再开始学习下一个级别。

AP体系学生

AP体系有CSA和CSP两门课程，如果同学们学的是CSA，那默认大家是掌握一定的编程基础，如会写Java，那同学们在备考的时候可能会时间会稍微短一点。如果是学CSP课程的同学们，可能知识储备相对比较弱，大家可以通过老师给定的推荐备考时间，结合自身的情况进行备考~这边建议大家预留出来3- 6个月的时间去复习。

AL体系学生

如果同学是A Level 体系的话，那么认为这些同学是掌握计算机理论和数据结构的理论知识的。相比AP课程体系对很多代码细节要求较高，而A Level课程体系要求自己写的代码会少很多，故老师认为同学们在备考第一个级别，即青铜升白银的时间会稍长一些，可能需要4-6个月。

IB体系学生

IB课程也是分两类，一个是HL，一个是SL。HL可能会掌握了一些数据结构和算法，如果说对于算法有一定的更深理解，那这里可能会时间会相对短一点。

对于HL的同学，在第一阶段在备考3个月或者4个月的基础上，还是能够达到晋级白银的水平。如果是SL的同学，基础相对较弱，因此要预留出来5到6个月做准备才会保险一点。