发布时间:2024-02-05 17:52:51 编辑:小杨来源:犀牛国际教育
American Mathematics Competition 8数学竞赛是一项美国初中数学竞赛,面向全球八年级及以下学生,在北京上海广州深圳等地,越来越多优秀的小学生也开始参加AMC8数学竞赛。该竞赛自1985年开始,如今已成为备受关注的中国数学竞赛之一,也是小初阶段最具含金量的赛事之一。
诸如:上海三公、北京六小强及许多国际学校在招生时也会将AMC8成绩单作为一项衡量学生数学水平的重要参考指标。
近三年AMC8考点分析
▼基础代数:多元一次方程、简单二次方程、简单不等式;简单数列;基本代数技巧、整数、有理数、无理数、实数、数轴和直角坐标系,
▼基础几何:圆,规则图形的周长和面积;基本平面几何技巧;规则立体几何图形、基础几何作图;平面欧氏几何,点、线三角形、特殊四边形、
▼基础数论:最小公倍数和最大公约数、同余问题、奇偶分析、整除的性质
▼基础组合:韦恩图,排列,组合和概率入门,阶乘和二项式系数、杨辉三角
2023年AMC8竞赛4大板块占比如下:
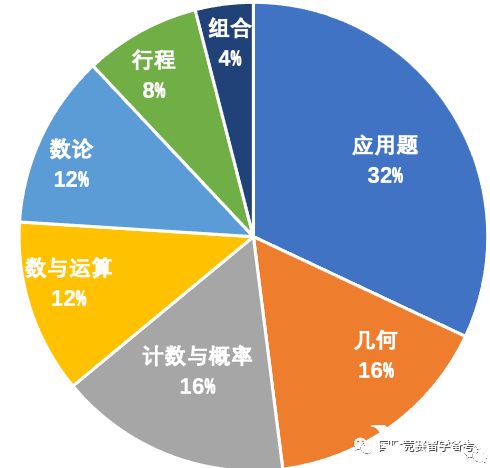
与2022年相比,2023年的AMC8竞赛试题继续加强了对代数内容的考察,其中有多道题需要运用字母和方程解法来解决问题。此外,传统AMC8喜欢考察的数论和组合计数内容也重新回归,使得第11-20题的难度增加。
这次竞赛的前15题注重细节考察,部分题目需要进行大量计算(考试时不能使用计算器)。最后3道题的难度较大,其中第23题是一道概率题,熟悉往年题目的学生可能可以用类似的思路解决;第24题是一道几何题;而第25题则考察了等差数列的运算,难度并不是特别大。
找规律
➤ 对于数列问题,最好从最简单的初始情况开始研究,以期发现规律。
➤ 许多余数求解问题中,余数往往呈现循环出现的模式,因此可以尝试寻找规律
特定值法
➤ 在题目要求寻找最大值或最小值时,通常从最极端的情况开始考虑,可以假设变量中的一个达到其极值。
➤ 在一些比例问题、百分比问题和比率问题中,当不知道总数且总数对题目答案没有影响时,可以假设一个总数来进行计算。
➤在几何图形不是唯一确定的情况下,可以假设特定条件(例如特殊角度或特定边长),然后进行计算。
排除法
➤ 考虑所求问题的可能取值范围,可以排除范围外的选项
➤ 逻辑推理问题通常可以逐个检验每个选项,排除其中存在矛盾的选项。
➤ 根据奇偶性,可以排除某些选项。
度量法
➤ 对于部分几何题,若题目条件能够唯一确定图形,可以绘制出标准图形。
➤当题目条件无法唯一确定图形时,可以绘制某种特殊情况下的图形,然后通过度量边长或角度直接得出答案。
AMC8对计算能力要求较高,要想取得佳绩,需要掌握8年级及以下的所有数学基础知识并且长时间习惯性练习。

犀牛根据学生的基础和目标不同,AMC竞赛课程大方向上分为Pre AMC8课程和AMC8直通车。
课程类型:4-8人小班 / 一对一
授课模式:线上线下同步开课,可回放。
授课语言:中英双语教学 / 纯英文授课


为3-5年级或具备3-5年级水平,想参加AMC8考试的学生提供AMC8课程。
课程目标:AMC8低龄成就奖(15分奖)





咨询AMC8培训后台私信客服

AMC04-17


物理碗04-23

物理碗06-05


化学竞赛01-11