AMC数学竞赛是什么?AMC数学竞赛难吗?AMC数学竞赛适合几年级学生?如何备考AMC数学竞赛?有没有AMC数学竞赛的历年真题?AMC数学竞赛考试内容有吗?考试大纲有没有?要怎么备考AMC数学竞赛?
AMC数学竞赛介绍
美国数学竞赛AMC是由美国数学协会MAA主办的美国国家级蕞重要的系列数学竞赛,由美国数学协会主办,是美国国家级别的系列数学竞赛。这项竞赛是为所有喜爱数学的学生所开发的,试题由简至难兼具,使任何程度的学生都能感受到参与竞赛的挑战,同时,赛程设置还可以筛选出在数学领域别具天赋的选手。对于想要申请理工科专业的学生来说,AMC竞赛能够极大提升大学的申请竞争力。如斯坦福、麻省理工、加州理工等名校都会把AMC成绩作为录取学生的重要指标。AMC也是美国中学校长每年重点推荐的活动之一。
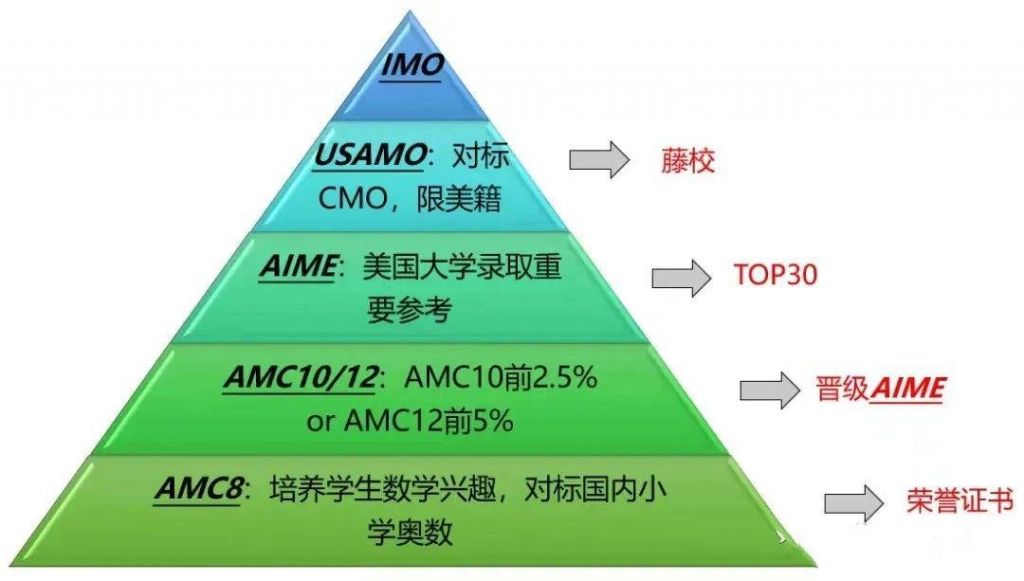
AMC美国数学竞赛分为三个等级,分别是AMC 8,AMC 10,AMC 12,AIME,USAMO\USAJMO,其中,在AMC10和AMC12竞赛中成绩优秀的学生被邀请参加美国数学邀请赛AIME,AMC和AIME综合成绩前270名的美国籍学生被选入参加美国奥林匹克数学竞赛USAMO,中国学生由于国籍限制,最终只能晋级到AIME阶段。
2010年-2022年AMC历年真题
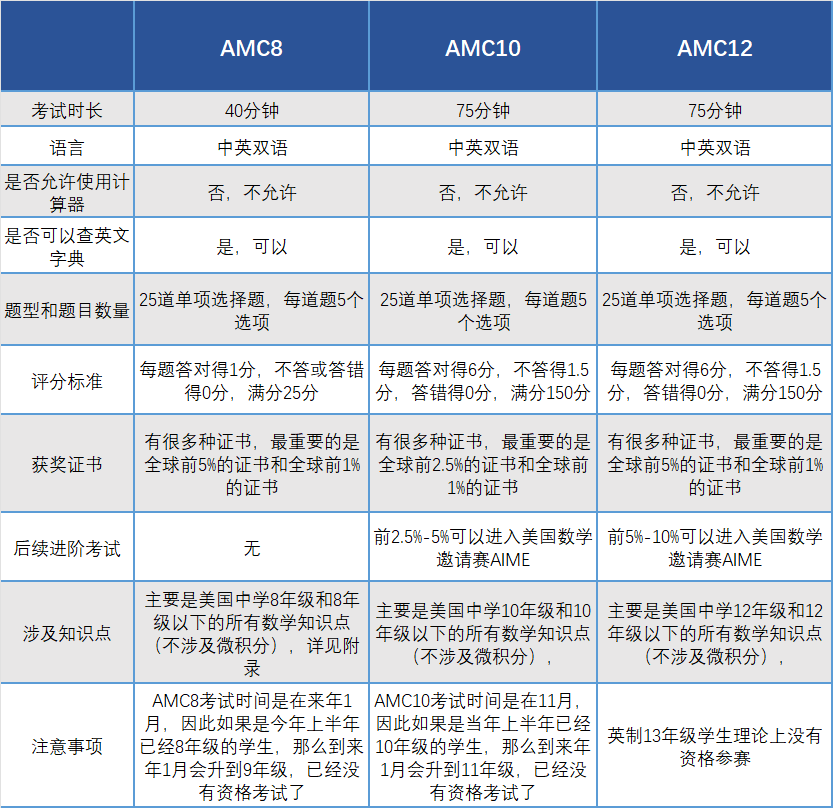
AMC8/AMC10/AMC12考试规则
AMC8/AMC10/AMC12在评分标准也有所不同:AMC8每题答对得1分,不答或答错得0分,满分25分;AMC10/AMC12每题答对得6分,不答得1.5分,答错得0分,满分150分。
AMC8/AMC10/AMC12区别还体现在一下多个方面,具体如图:
牛娃妈妈-AMC竞赛上岸经验分享
AMC8/10/12 前1%
1. 对于给孩子的AMC备考,我制定了周密的规划。首先花了5个月的时间,自主学习AMC8/10的知识点(对于基础薄弱或者自学能力较差的学生建议从基础课程开始学习)。然后,给孩子报了强化冲刺班上学习了两个月,培养了孩子在面对难题时的数学思维能力。孩子说在练习题方面,专业的教辅材料帮助很大。
2. 核心概念和公式定理一定要熟,建议在学完每个知识点后,在历年真题中挑出对应的题进行专项检测,切勿盲目刷题。
3.AMC12比AMC10要难不少,所以我们AMC12是选择了一对一,一对一的老师有时间根据孩子的实际情况制定相应的学习计划,找到孩子思维的漏洞,提升的效果也更显著。
很多高分的美国学生早在小学就开始准备AMC了。对国内学生来说,如果想要在AMC比赛中取得好成绩,建议至少提前半年开始准备,蕞好的话能提前一年开始准备以达到更好的成果!!
AMC8/AMC10/AMC12备考要点
AMC数学竞赛备考时,AMC8/AMC10/AMC12竞赛考察的备考内容也不尽相同,难度逐级递增。
AMC8竞赛考点:
基础代数:整数、有理数、无理数、实数、数轴和直角坐标系;多元一次方程、简单二次方程、简单不等式;简单数列;基本代数技巧。
基础几何:基础几何作图;平面欧氏几何,点、线、三角形、特殊四边形、圆;规则图形的周长和面积;基本平面几何技巧;规则立体几何图形。
基础数论:奇偶分析、整除的性质、最小公倍数和最大公约数、同余问题。
基础组合:韦恩图;排列、组合和概率入门;阶乘和二项式系数、杨辉三角形。
AMC10竞赛考点:
进阶代数:多项式,余数定理,韦达定理,根与系数的关系,特殊高次方程;进阶不等式、均值不等式;函数入门,定义域和值域、二次函数、指数函数、对数函数、简单三角函数;数列进阶;代数技巧进阶。
进阶几何:进阶几何作图;三角形进阶、正弦定理、余弦定理、内切圆和外切圆、斯图瓦尔特定理、共点和共线;圆和四边形,四点共圆,圆的外切四边形;正多边形,角度,周长和面积;进阶平面几何技巧;解析几何入门。
立体几何:点、线、面的关系,三维坐标系;立体几何作图;正多面体,欧拉公式;特殊的立体几何图形,立体几何技巧。
进阶数论:数,数组和序列;模运算,复杂同余问题;整数、分数和小数,进制转换;基本丢番图方程,进阶数论技巧。
进阶组合:容斥原理;二项式定理及相关结论;进阶排列、组合和概率;期望入门,递推、二分法,进阶组合方法。
AMC12竞赛考点:
涵盖所有高中部分的数学知识,在 AMC10 基础上新增知识点:
进阶代数:复杂不等式、调和不等式、轮换不等式、柯西不等式;复杂函数问题,反函数和符合函数,三角函数和差化积、积化和差,万能公式;复数,复平面,欧拉公式,蒂莫夫公式;数学归纳法、复杂数列和极限。
进阶几何:圆相关几何进阶;数形结合,二维、三维图形的函数表达,进阶解析几何;不规则二维、三维图形的处理;二维向量,三维向量。
进阶数论:二次余数,高次余数、费马圣诞节定理、费马小定理;各类丢番图方程的解法。
进阶组合:随机过程和期望。复杂组合问题技巧。