课程咨询热线 400-656-1680
发布时间：2024-02-07 10:46:21 编辑：Mila来源：网络
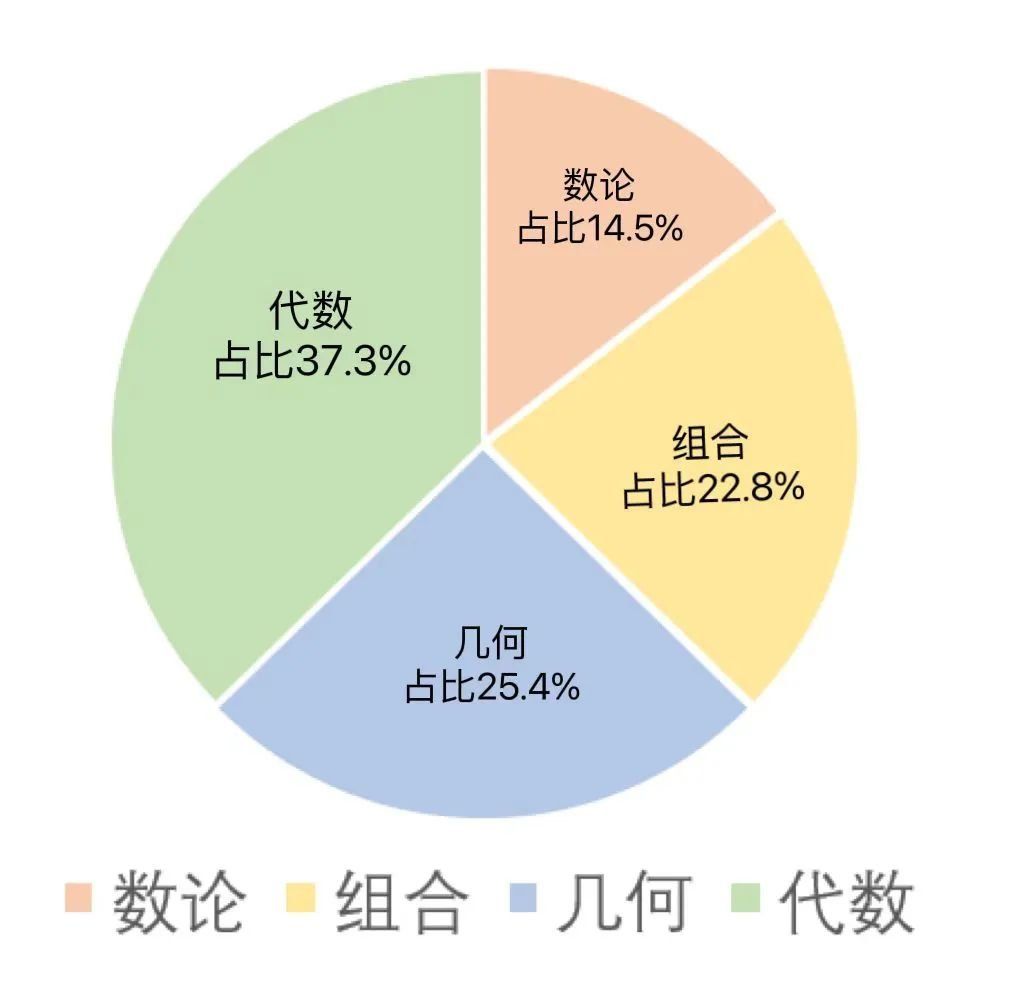
AMC10/12数学竞赛试题主要分为4个模块：代数、几何、数论、组合。每个模块考察的内容不同，占比也不同。攻破这四大模块，那么你距离AIME晋级也就不远了。今天我们通过探究真题，带领同学们呢体会AMC的命题风格，巧破难题！
AMC10/12数学竞赛
AMC10/12历年真题：
真题解析
解析：在这个题里面，N和M虽然实际上是确定的数，但是以未知数的形式出现的。要先根据条件列出一个不定方程，因为不定方程在限定条件是可能有唯一解或者有限定个数的解的，题中N和M都是整数，N>2M和M>4，这些限定条件排除了不可能的解，剩下的就是我们要的解。
几何占比第二多，大概6-8 题，比较注重平面几何、三角形与四边形的考察。大部分内容在国际课程中不涉及，所以对于国际学生来说可能会有点陌生。下面以一道真题为例：
解析：从图形上来看，一个正方形被两条直线分割成了4块，我们注意到其中3块都是三角形，所以我们只要知道这3个三角形的面积比例，不规则四边形AFED也就知道了，答案自然而然就出来了。
组合是每年的必考点，大概占比5-6题。其中排列和组合是组合数学的基本概念，而概率又是由排列数和组合数进行“排列组合”，也就是加减乘除各种运算而得到的。只要概念清晰，方法系统化，可以说理论上一切的概率问题都可以计算出来。下面我们通过一道真题详细了解一下：
解析：首先，五个顶点我们视为不同的，所以对它们的涂色是有顺序的。关键是要把顺序排列好，还要把情况分解好。我们用下面的树形图来表示。把每一个分支的计数算出来，最后加和就是总数了。
解析：这个题的正规解题方法要用到费马小定理和中国余数定理，如果能掌握这些当然很高超。但是即使不会这两个定理，也可以用几次WLOG（without loss of generality，不失去一般性）的特例推理，进行解答。
AMC数学竞赛备考课程
课程类型：一对一辅导/4-8人小班课
授课模式：线上/线下同步授课，有课程回放录像可供复习
AMC04-17
物理碗04-23
物理碗06-05
化学竞赛01-11
