发布时间:2024-11-14 11:04:33 编辑:Mila来源:网络
2024年AMC10/12A卷和B卷考试已经全部结束啦!接下来有望晋级AIME的同学们,就要开始认真备考啦!因为AIME考查的内容远超AMC10和AMC12的基础知识,涉及更高难度的定理和高级技巧。那么AMC10、AMC12晋级AIME分数线是多少?2025年AIME竞赛考试时间怎么安排的?AIME培训课程哪家好?
2024AMC10/12晋级AIME分数线
我们以2023年的AMC10/12竞赛考试分数线为例,可以看出:

由上图2023年晋级AIME的历年分数线可以看出:
2023年AMC10A卷晋级AIME分数线为103.5分,需答对17题及以上;
AMC10B卷晋级AIME分数线为105分,需答对18题及以上,相较于前2022和2021年分数线有增长;
2023年AMC12A卷晋级分数线为85.5分,需要答对14题以上;
B卷晋级分数线为88.5分,需要答对15题以上,近年来晋级AIME的分数线波动不大。
由此可以看出,2024年AMC10、AMC12晋级AIME至少需要达到以下分数:
AIME晋级分数线
AMC10竞赛晋级AIME,需要至少105分左右
AMC12竞赛晋级AIME,需要至少88分左右
2025年AIME竞赛考试时间安排


01
AIME报名截止时间
AIME I :2025年1月28日截止报名
AIME II: 2025年2月4日截止报名
02
考试时间
AIME I :2025 年 2 月 6 日(美东时间)
AIME II :2025 年 2 月 12 日(美东时间)
03
考试时长
3小时
04
考试语言
中英文双语
05
考试形式
线上考试
06
试卷构成
15道填空题,答案为000-999之间的整数,不允许使用计算器
07
计分方式
满分15分,答对1题得1分,答错、未答不得分
08
考试范围
除去微积分外的中学数学知识,但允许使用微积分方法解题。
09
参与方式
AMC10/12 分数达到晋级线后即可获组委会邀请参与AIME邀请赛(考生会收到官方邮件/短信通知)。
2024年AIME培训课程
联系客服
获得1V1服务
AIME竞赛如何备考
AMC10/12晋级aime后,要补充哪些知识才能拿AIME高分?
总体来说,AMC 10和AMC 12考题难度更倾向于基础定理的理解与应用,几乎不会涉及上述高级定理和复杂技巧。
AIME考查的内容远超AMC 10和12的基础知识,涉及更高难度的定理和高级技巧。这些知识要求学生在数论、代数、几何、组合数学、递推数列及排列计数等多个方面具备深厚的理解与灵活应用能力。
数论
AMC 10/12:主要考查基础的整除性、因数分解、余数定理等。例如基础的整除性规则、偶奇性判断、最大公约数与最小公倍数。
AIME: 涉及更复杂的数论定理与技巧。
·费马小定理和欧拉定理:常用于复杂的同余问题、指数模运算等题目。
·莫比乌斯反演和中国剩余定理:解决多重同余和特定的整除性问题。
·丢番图方程:即求整数解的问题,尤其是涉及多重限制的方程题目。
代数
AMC 10/12:考查基础代数知识,如一次和二次方程、根的性质、简单多项式展开等。
AIME: 代数内容更加深度和复杂,要求学生灵活运用高级技巧。
韦达定理的应用:要求学生在多项式题中灵活运用根和系数的关系。
复数平面和复数根:包括复数的几何表示及共轭根关系,考查学生理解复数在平面中的变换。
二项式定理的高级应用:不仅限于整数幂,还涉及分数或负数幂的展开及组合性质。
几何
AMC 10/12:几何考题主要集中在基础图形的面积、角度、相似性及平行四边形、三角形和圆的基本性质。
AIME: 几何难度显著增加,要求对复杂图形及其属性有深入理解。
Euler线、九点圆:涉及三角形的特殊点及其性质。
Heron公式的高级应用:尤其在不规则三角形中计算复杂面积。
复数平面的几何应用:例如复数旋转、缩放,考查复数作为几何变换的工具。
组合数学
AMC10/12:组合题目通常基于排列组合基础,例如基本的计数法、排列组合定理。
AIME: 组合题目在计数方法及递推上要求更高。
包涵-排除原理的复杂应用:尤其是涉及多重条件限制的计数问题。
递推关系与特征方程:在求解复杂数列或组合问题时使用特征方程法推导递推关系。
Catalan数和斯特林数:用于处理某些特定的分布问题,特别是与括号匹配、树形结构相关的题目。
AIME竞赛培训课程
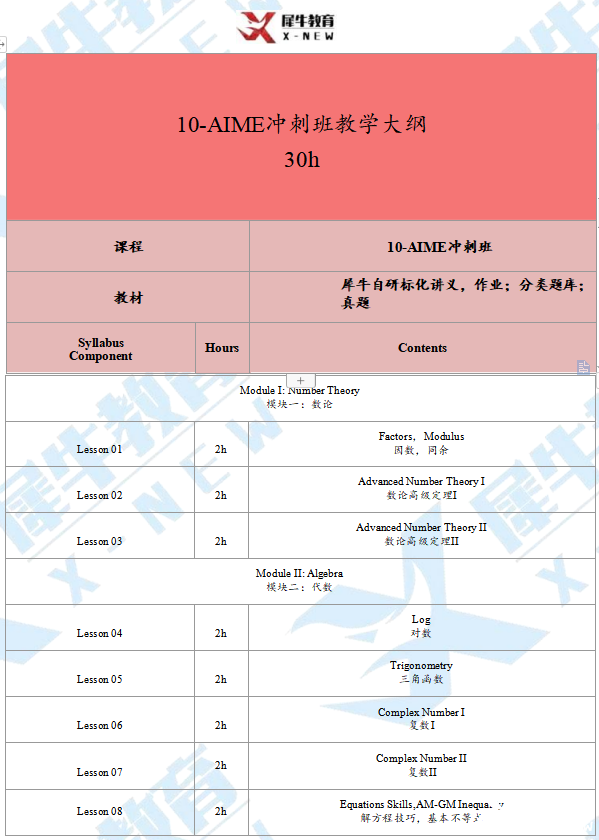
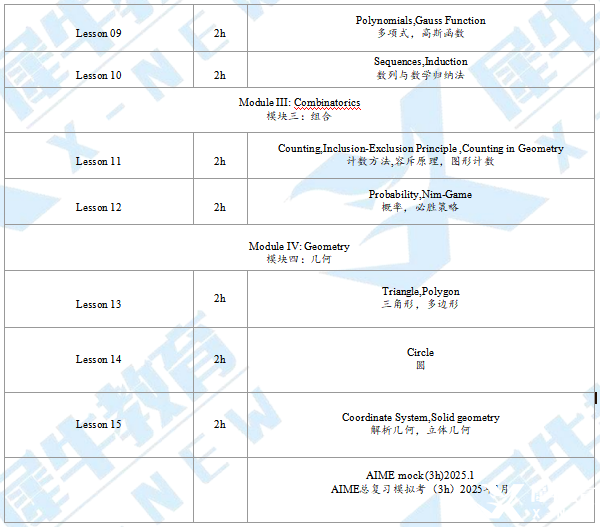
犀牛AIME竞赛培训课程大纲:
AIME培训课程师资展示:


AIME班型设置:6-12人班/一对一
AIME授课语言:中英双语/纯英文
AIME授课形式:线上/线下课程(支持回放学习)
AIME线下授课:面授互动
北京/上海/深圳/广州/天津/苏州/无锡/南京/杭州/青岛/成都/宁波/武汉/合肥……
AIME培训课程
联系客服
获得1V1服务

AMC04-17


物理碗04-23

物理碗06-05


化学竞赛01-11