上海AMC12竞赛培训长线班！

上海犀牛AMC12数学竞赛直通车培训内容继续招生！你可以选择英语或中英双语授课！2024年AMC12数学竞赛考试已经结束。如果你错过了考试或成绩不令人满意，犀牛将为AMC12数学竞赛提供培训直通车课程，帮助学生系统地巩固数学基础，提高他们的数学思维能力和解决问题的能力。那么犀牛的AMC12竞赛培训直通车课程是怎么安排的呢

AMC12数学竞赛难度怎么样?

AMC12数学竞赛是美国数学竞赛(American Mathematics Competitions，简称AMC)系列中的一项，由美国数学协会(MAA)主办，面向12年级及以下的学生开放。AMC12是晋级美国数学邀请考试(AIME)的重要途径，同时也是申请名校时的加分项。

AMC12数学竞赛的题目难度分布通常按照由易到难的顺序排列，可以分为以下几个部分：

这些题目主要考察学生对数学基础概念和公式的掌握程度，包括代数基础运算、几何图形的基本特性、概率论的基本理念等。

解题策略是重视对数学关键概念和基础公式的整理与记忆。

✔ 中等难度题（11-20题）

从第11题开始，难度逐渐提升，融入了更高级的数学理念与解题方法。涉及复杂代数方程求解、几何证明、排列组合等问题。这部分题目比较有深度，难度增大，且题目考查形式较为灵活。

解题策略是进行专项训练，重点攻克那些具有代表性的题目类型。

较高难度题（21-25题）

最后几道题目通常是整个考试中最难的部分。这些题目要求学生具备一定的综合分析能力和解题技巧。难度非常高，通常只有少数顶尖选手能够完全解答。

解题策略是按照专题进行复习，多刷类似题目，培养构造和转化问题的能力。

 总的来说，AMC12的题目难度分布是逐渐增加的，前10题为基础题，11-20题为中等难度题，21-25题为高难度题。考生在备考时应根据自己的实际情况，对不同难度的题目进行针对性的复习和练习。

AMC12数学竞赛直通车培训课程

X-NEW

 

AMC12数学竞赛直通车培训课程开课时间安排

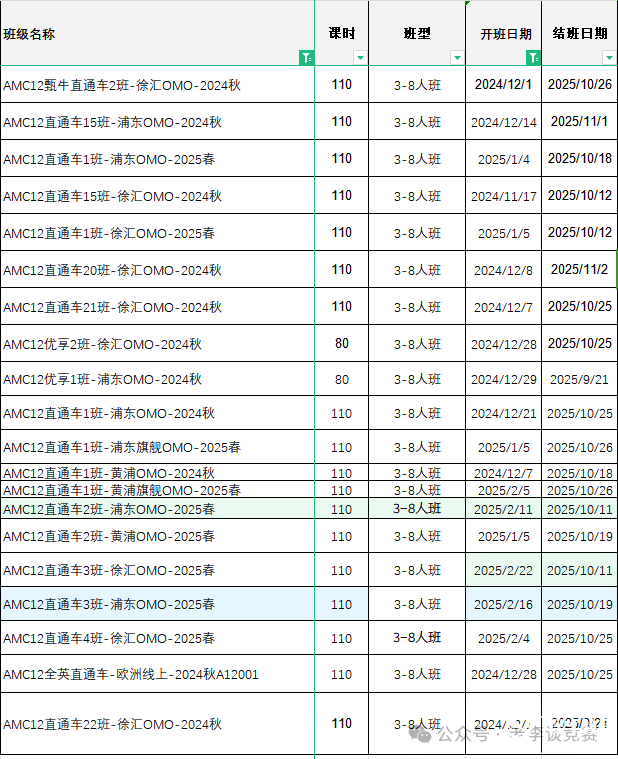
课时：AMC12数学竞赛培训直通车：110h

AMC12数学竞赛培训优享班：80h

授课班型：3-8人/可自组班

开班时间：滚动开班

授课语言：全英/中英双语授课

授课方式：面授/在线

在线授课平台：classin

线下授课校区：北京、上海、深圳、苏州、无锡、南京、杭州、青岛、天津、成都、重庆、大连、宁波、香港、广州等

 

AMC12数学竞赛培训师资介绍

犀牛AMC12竞赛培训课程有毕业于清北复交、纽约大学、曼彻斯特大学、墨尔本大学、香港理工大学的一系列牛师授课，人均授课时长2000小时+，竞赛体系出身，深耕国际教育多年，带出了很多AMC12竞赛优秀学员。

王老师——斯坦福大学统计系硕士学位

高中时曾获AIME 14分;主要从事AMC/AIME等数学竞赛的教学，ITCCC官方认证的Duke Math Meet教练

教学时长5年，指导超过200名学生进入AIME，20多名学生进入USAMO，指导超过65%的学员进入AIME

曾辅导多名学生进入Ross/Sumac等顶尖数学夏校。

严老师——伦斯勒理工学院数学系学士学位，GPA3.96.纽约大学数学系研究生，数学科目全A毕业;SAT、GRE数学部分、AP微积分BC均为满分，高中参加AMC，AIME均获得高分

教龄4年，累计授课时长5000+小时

辅导多位学员各类学科考前快速提分，AMC与欧几里得数学竞赛多位学员取得优异的成绩。AMC12.AMC10.80%学员成功晋级AIME并取得优异成绩，最高分学员136.5分。欧几里得竞赛90%的学员成绩前25%，并有部分学员成功获得horor roll，最高分94分。

刘老师——美国罗切斯特大学数学博士，北京大学数学学士

曾获高中数学联赛一等奖

英语流利地道，可全英授课

3年国际数学竞赛授课经验，累计教学时长3000+小时;辅导多名夏校学生取得优异成绩，众多学生在AMC10、12中获得前1%的成绩

李老师——伦敦大学学院数学系

欧几里得竞赛奖项获得者

高中业余双轨兼修A-level课程并取得A*A*A成绩

教学时长4年，累计教学时长6000+小时，熟悉AMC等各类国际数学竞赛

多名学生在各类国际数学竞赛中获得证书，超百名学生进入英国G5.美国常春藤等世界顶尖名校;

 

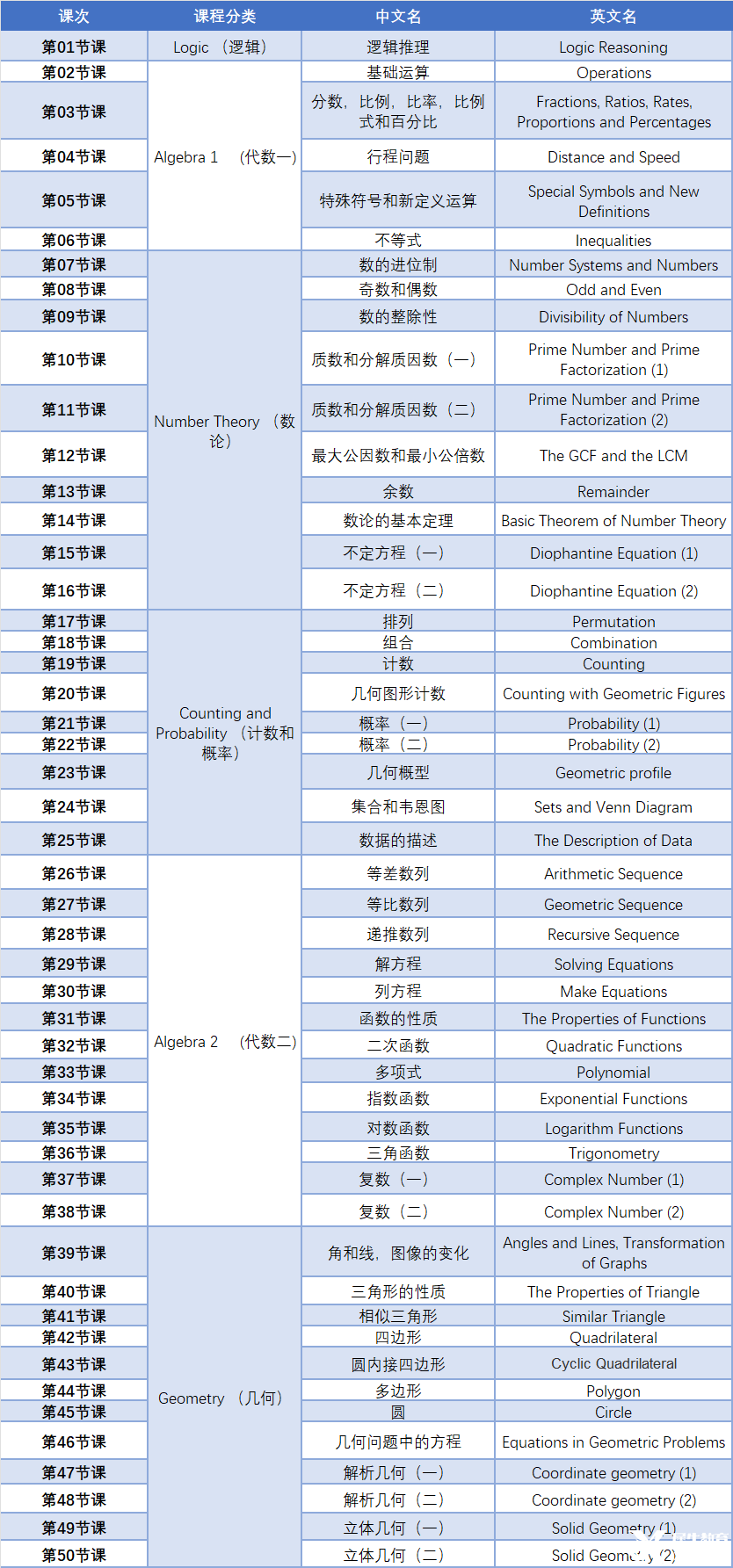
AMC12数学竞赛培训课程大纲

犀牛AMC12培训大纲采取分段式教学，能够帮助学生清晰把握每个阶段学习的重难点。

2024年AMC12数学竞赛考情分析

X-NEW

 

AMC12数学竞赛A卷考情回顾

2024年AMC12数学竞赛A卷的考试难度和去年基本持平。

整体考点分布上，AMC12四部分题目数量分别为4道、14道、4.5道、3.5道

- 数论占比对比往年大幅上升，考察很多不定方程

- 三角函数考察很多，考察计算基本功

- 代数难题计算量大，没有考察复数

- 总体难度和往年相对较持平

1. 代数与函数部分

- 题目数量适中，函数部分的难点主要集中在函数的对称轴和对称性上。

- 基础题和中低档题目难度不高，但难题以代数为主，提升了整体难度。

 基础题和中档题 - 7道

- 第1题：基础代数运算化简，难度低。

- 第6题：向量加法运算，新颖但难度低。

- 第7题：平均数计算，难度低，通过列方程求解。

- 第9题：对数与三角函数结合，难度适中，需要熟悉对数运算和三角函数周期。

- 第12题：函数对称轴问题，观察对称轴位置，可使用导数，对称轴横坐标处导数为零。

- 第15题：看似组合题，实为等差数列性质考察，需要观察和计算能力。

- 第16题：韦达定理使用和计算，需要代数变形，快速方法为使用复数将平方和转换为复数平方差。

 高档题 - 2道

- 第22题：递推数列问题，通过改变递推公式形态求解，属于高档题中较简单。

- 第25题：整系数有理一次函数的自反对称性和组合计数综合，需求反函数，列方程讨论，难度高但思路明确后不难。

2. 概率、计数与数论

- 前20题数论题量较大，不定方程题型多，后5题无数论题，提高了前20题的难度;A卷组合计数题量少，难度不高。

数论部分基础题和中档题 - 6道

- 第3和4题简单，第5题需细心避免漏算。

- 第11题：技巧性题目，分析b/720最接近1的情况，选择质因子幂。

- 第14题：数的进制转换，技巧性不强，较简单。

- 第19题：不定方程问题，难度大，需代数变形、因式分解和整除性分析。

 组合计数部分 - 3道

- 前20题组合计数问题少，第14题考古典概型，难度低。

- 第20题：找规律的组合计数问题，难度大，但不及数论部分。

- 第21题：与平面几何结合考察几何概型。

3. 几何

- 本次几何高档题难度未特别突出，特点是对三角恒等变形的考察力度加大。

 几何部分低中档题 - 3道

- 第7题、17题和第18题涉及几何，其中第18题为纯平面几何(四点共圆)，其余两题要求高三角函数计算和恒等变形。

 几何部分高档题目 - 2道

- 第22题：与几何概型结合，难度大。

- 第24题：四面体立体几何问题，需耐心辅助线绘制。

 

2024年AMC12数学竞赛B卷考情回顾：

整体来看，B卷的考试难度比 A卷低，考过的学生都反应B卷的发挥比A卷 要好，这也意味着B卷的考试分数线可能相对较高。对比2023年整体题型及涉及知识点的范围和往年没有太大区别，主要区别在知识占比、整体难度以及题目难度的变化。

1. 代数与函数部分

- 第1至7题涉及了基础的阶乘运算、进制转换和代数表达式处理，整体难度较低。

- 第8题探讨了对数运算，需要掌握对数取倒数的规则，并运用韦达定理，难度属于中等。

- 第10题关于平均数和中位数的计算，需要通过列方程和枚举法求解。

- 第11题是三角函数求和问题，通过头尾配对简化计算。

- 第15题应用鞋带定理计算三角形面积，属于解析几何范畴。

- 第17题涉及多项式整数解，利用有理根测试规则简化计算。

- 第18题是斐波那契数列问题，关键在于发现规律而非强行推导通项公式。

- 整体而言，代数与函数部分的难度较为适中，与A卷相比有所降低。

2. 几何部分

- 第7题通过割补法计算面积，较为简单。

- 第15题再次应用鞋带定理，不熟悉该知识点的学生可能需要更多时间。

- 第19题通过连接中心和顶点，使用割补法和三角形面积公式求解。

- 第20题关键在于找出三角形面积最大化的条件，无需列出函数表达式。

- 第21至24题为几何综合题，涉及数论知识，对代数和几何知识的综合运用要求较高。

3. 运算

- 涉及三角形的重要性质，如内接圆半径、面积计算和正余弦定理，要求对这些知识点有较高熟练度，但与去年的难题相比，难度持平或有所降低。

4. 复数部分

- A卷未涉及复数，而B卷考查了复平面几何问题，通过割补法和三角形面积求和计算，难度适中，但计算量较大。

5.组合计数与概率

- 前20题中包含四五道此类题目，难度不大，但需要严谨的分类讨论。

- 最后一题涉及独立事件和伯努利试验的概率计算，理解题意是难点，分类讨论不难，但计算量较大。

- 压轴题的难度相较于往届有所下降。

在内容分布上，代数和函数的比重有所提升，特别是在B卷中，几何部分的比重显著增加;复数部分的题目数量有所减少。

就难度而言，基础题(评分为1分的题目)的数量相对减少，中低档题和中档题的难度有所上升，中高档题的难度有所下降，难题的数量减少，但计算量相较于去年有所增加。

具体到知识点的分布，B卷的中高档题目主要集中在几何和组合概率两个领域，数论部分仅考察了基础题和中低档题，复数部分没有出现难题，概率和计数题目的整体难度有明显降低。

相较于去年，今年最难题目的难度保持不变，但与A卷相比，整体难度有所下降。整张试卷的考点较为传统，鞋带定理的考查标志着一个旧考点的重新回归。与A卷相比，B卷整体上显得更为保守，缺乏新颖和出人意料的考点，这符合B卷一贯的风格，即创新题目和奇特题目较少，而常规题目占据较大比例。

AMC12数学竞赛历年分数线

X-NEW

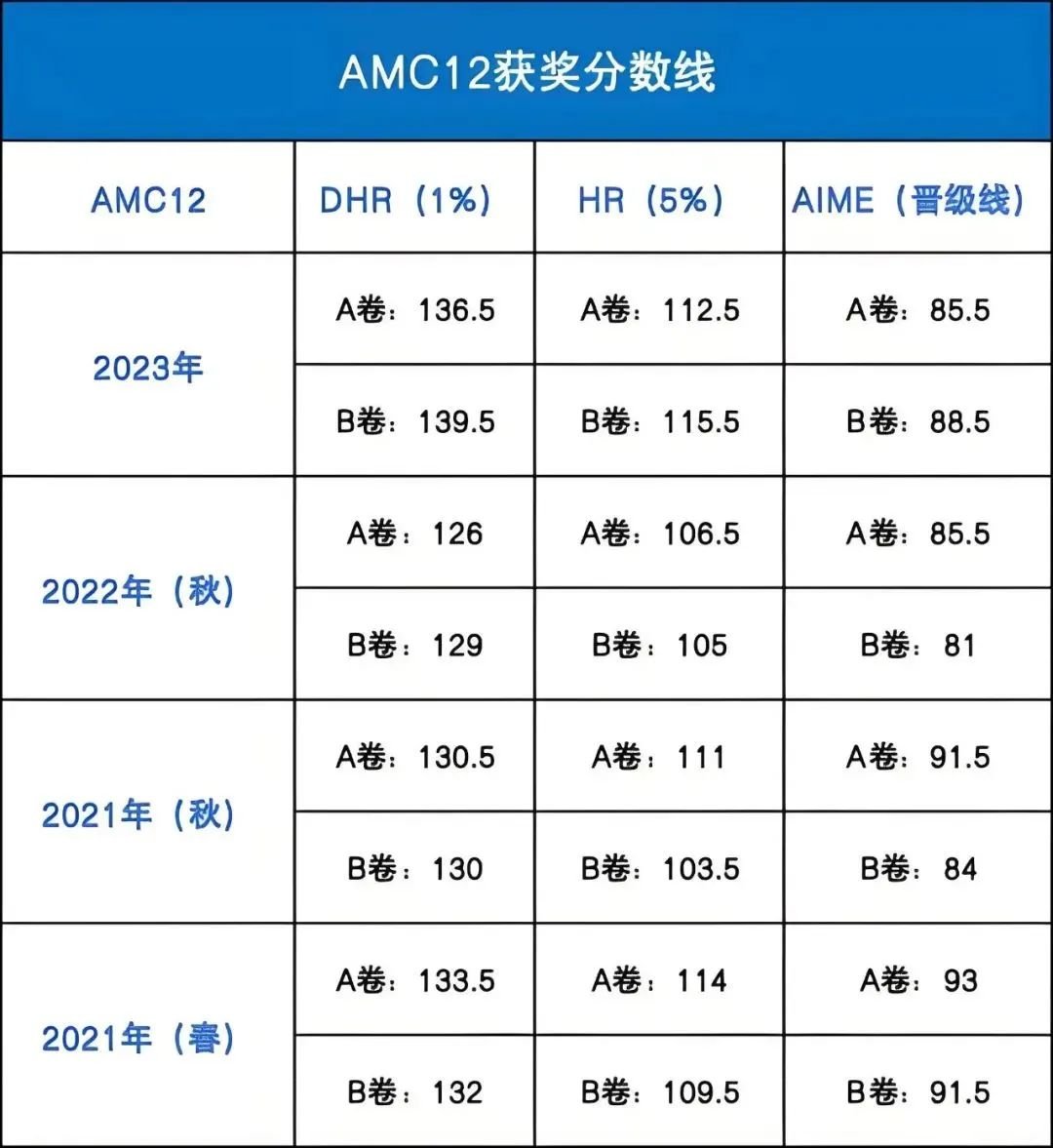
根据近三年的趋势，要晋级美国数学邀请赛(AIME)，A卷考生通常需要达到85至90分，而B卷考生则需要88至95分。

要在全球范围内排名前5%，考生大约需要获得100至110分，这要求考生具备较强的数学综合实力，能够妥善处理大多数题目。

至于全球前1%的高分，考生通常需要达到125至135分，这样的成绩表明考生在数学学习上拥有非凡的才能和出色的解题技巧。