2025年AMC8会变难？AMC8考点分析及备考规划详解

　　2025年AMC8竞赛距离开考剩下的时间已经不多了， 那么今年的考试题会不会变难呢?基础数论、基础代数、基础几何、基础组合的占比会有怎样的变化?本文我们针对AMC8竞赛分享一些内容，希望对大家能够有所帮助!

　　2025年AMC8竞赛难度分析

　　2023年AMC8试题难度加大，主要是因为增加了数论和组合计数内容;2024年考题难度下降，没有涉及到太多高年级知识点，其他考点内容难度也有所下降。趋势是难度越来越大，初中知识越来越多。需要超前学习竞赛知识点，去拓宽AMC 8常考知识点的深度以及广度。

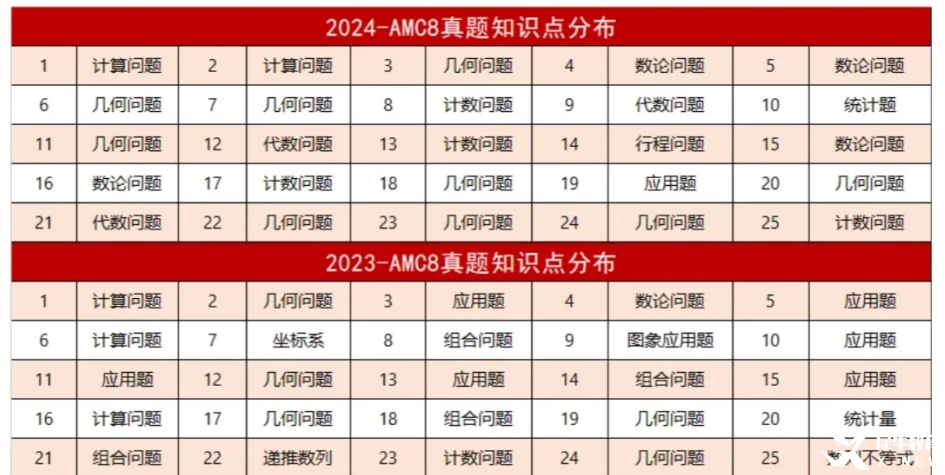
　　在 AMC8 竞赛的发展进程中，组合题呈现出多维度的演进态势。

　　排列组合题通常会整合多种数学思维类型，要求学生构建易于自身理解的思维架构与模型，并能够灵活且恰当地加以运用。回顾历年 AMC8 竞赛中的排列组合与概率题，其并非处于高难度层级，学生借助多次反复的练习与尝试，往往能够实现正确解答。

　　通过对近年来 AMC8 竞赛真题的深入剖析，可以清晰地洞察到数论题的难度呈现出逐步递增的趋势，而几何题的数量亦呈现出增多的态势。

　　基于此，考生在备考过程中应着重聚焦于组合、数论以及几何这几个关键领域，因这几个领域在竞赛整体中的比重已有所上扬。

　　2025 年 AMC8 竞赛考察重点

　　几何题目的占比预计会大幅提升，极有可能占据所有题目近一半的份额。

　　例如在 2024 年的考试里，共计出现了 10 道几何题，尤其在最后 5 道题目中，竟有 3 道为几何题。

　　与之形成鲜明对比的是，代数板块的比重显著下降，2024 年该板块题目的数量仅为前两年的一半。

　　计数板块的题目一贯以高难度著称，在过往考试中往往仅现身于最后几道题目之中。

　　此外，数论部分的难度依据趋势推测仍会进一步增大。考生需精准把握这些变化趋势，针对性地制定备考策略，以提升在 2025 年 AMC8 竞赛中的表现与成绩。

　　数列专题

　　在 AMC8 竞赛的数列考查范畴内，等差数列占据着极为关键的地位。其中，等差数列的求和以及求特定项的运算往往成为众多考生的易错雷区。考生于此类题目出错，多源于计算环节的疏忽或审题过程的不严谨。实则，等差数列的通项公式与求和公式乃是攻克此类问题的核心利器。通项公式能够精准确定数列中任意一项的值，而求和公式则可高效计算数列前若干项的总和。唯有考生通过大量针对性练习题的深度研磨，方能在实战中对公式运用自如，从而有效规避这些常见错误，提升解题的准确性与效率。

　　分数中的比与比例板块

　　分数中的比与比例这一知识点在 AMC8 的应用题领域频繁现身。考生在此类题目面临的首要挑战便是如何正确构建数学表达式。处理分数相关问题时，分数的灵活转换以及比例关系的精准把握堪称重中之重。正确的列式不仅是解题的起始关键，后续严谨且准确的计算步骤更是确保得出正确答案的必备要素。考生需对分数与比例的基本概念及其相互关系有着透彻的理解，并在实际解题过程中不断积累经验，方能在面对此类题目时做到游刃有余。

　　代数领域

　　代数部分于 AMC8 竞赛中主要聚焦于对考生计算功底以及方程法运用能力的检验。常见失误集中于计算失误与列式偏差这两大方面。代数题目对考生的计算精准度有着严苛要求，同时，对方程、不等式等基础概念的深刻领悟亦是不可或缺。方程法作为解决代数问题的核心策略，要求考生能够依据题目条件准确构建方程或不等式模型，并通过扎实的计算能力求解。大量的练习实践能够助力考生强化计算技能，深化对概念的理解，进而显著降低错误率，在代数板块斩获佳绩。

　　几何范畴

　　几何部分在 AMC8 竞赛里着重围绕三角形、四边形以及圆的面积相关问题展开深入考查。此中，等积变形这一几何变换技巧尤为关键，考生需善于通过图形的巧妙变换挖掘隐藏的数量关系。看图找数量关系能力则考验考生对几何图形性质与定理的熟练运用程度，能够从图形的直观呈现中敏锐捕捉到解题所需的关键数据与逻辑联系。割补法作为一种常用的解题手段，可将复杂图形转化为易于计算面积的简单图形组合。此外，良好的作图能力亦不容忽视，精准的作图有助于考生更直观地理解题目，发现解题思路。同时，三角形的相似形、勾股定理、全等以及中位线等知识点也是高频考点，考生需对这些几何知识要点融会贯通，形成系统的解题思维体系，以应对几何部分的各类挑战。

　　整除性考点

　　整除性作为数论板块的重要考点，在 AMC8 竞赛中常常使考生陷入困境。考生出错的根源多在于对常见整除特征的生疏。整除性问题的破解之道在于熟练掌握各类整除规则以及带余除法的运算原理。整除规则犹如一把把钥匙，能够帮助考生快速判断一个数是否能被另一个数整除，而带余除法则在处理非整除情况时发挥着关键作用。通过丰富多样的练习题训练，考生能够将这些整除性知识内化为自身的解题本能，从而在面对数论中的整除性问题时做到准确判断、高效解题，避免因知识盲点而导致的失误。

　　其他关键注意事项

　　（一）求和问题

　　等差数列的求和在 AMC8 竞赛中无疑是重要的计算枢纽。考生不仅要牢记求和公式，更要深入理解公式背后的数学原理，以便在不同情境下灵活运用。无论是直接运用公式计算给定等差数列的和，还是结合其他知识点解决综合性求和问题，都需要考生具备扎实的基础和敏锐的思维转换能力。

　　（二）应用题

　　解答 AMC8 中的应用题时，细致入微的阅读习惯与精准无误的题意理解能力是成功解题的基石。考生需逐字逐句剖析题目所传达的信息，将实际问题准确转化为数学模型，并进行合理列式。这一过程考验考生的文字理解与数学抽象能力的协同运作，唯有通过大量练习，才能在复杂的应用题情境中迅速捕捉关键信息，构建正确的解题思路。

　　（三）图形结合题目

　　图形结合的题目在 AMC8 竞赛中占据相当比例。此类题目要求考生具备敏锐的观察力与深入的分析能力。考生需仔细审视图形的形状、大小、位置关系等要素，从中挖掘出隐藏的数学信息，并与题目中的文字条件相互呼应。通过对图形的深入分析，考生能够更直观地理解问题的本质，找到解题的突破口，进而运用相应的数学知识求解。

　　（四）手工操作题目

　　部分 AMC8 题目涉及手工操作元素，这对考生的实践准备与应变能力提出了特殊要求。考生在日常备考过程中，应注重培养自身的动手操作意识与能力，对于可能出现的折纸、裁剪、拼接等操作类型题目有一定的心理预期与应对策略。在考试中遇到此类题目时，能够冷静应对，依据题目要求有条不紊地进行操作与分析，从而得出正确答案。