发布时间:2025-01-16 09:36:47 编辑:Daisy来源:网络
2024AMC8真题在哪里可以看?本文整理了完整版AMC8真题,还有详细的解析,帮助有需要的同学,还有历年真题及答案
What is the ones digit of?
求下列算式结果的个位上的数字。(计算:基本运算)
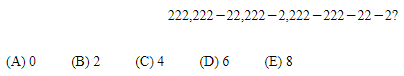
What is the value of this expression in decimal form?
把下列算式的结果写成小数形式是单位?

Four squares of side length 4, 7, 9, and 10 units are arranged in increasing size order so that their left edges and bottom edges align. The squares alternate in color white-gray-white-gray, respectively,as shown in the figure. What is the area of the visible gray region in square units?
四个边长分别为4、7、9和10单位的正方形按边长递增的顺序排列,使得它们的左边缘和底边缘对齐。正方形交替填充为白色和灰色,如下图所示。灰色部分的面积是多少平方?

When Yunji added all the integers from I through 9, she mistakenly left out a number. Her incorrect
sum turned out to be a square number. Which number did Yunji leave out?
当Yunji从1加到9的时候,不小心遗漏了一个数字。使得错误的和是一个平方数。那么Yunji遗漏的数字是多少?
(A)5 (B) 6 (C) 7 (D) 8 (E) 9
Aaliyah rolls two standard 6-sided dice. She notices that the product of the two numbers rolled is a
multiple of 6. Which of the following integers cannot be the sum of the two numbers?
掷了两个标准六面骰子。她发现掷出的两个数字的乘积是6的倍数。以下哪个整数不能是这两个数字的和?
(A) 5 (B) 6 (C) 7 (D) 8 (E) 9
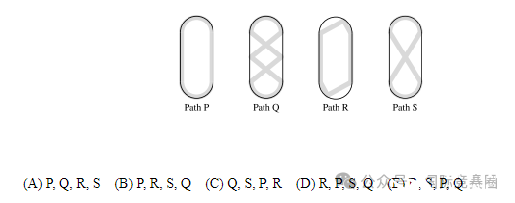
Sergei skated around an ice rink, gliding along different paths. The gray lines in the figures below
show four of the paths labeled P, Q, R, and S. What is the sorted order of the four paths from shortest
to longest?谢尔盖在溜冰场周围滑冰,沿着不同的路径滑行。以下图形中,灰色线条显示了四条路径P、Q、R和S。按照从最短到最长的顺序,这四条路径要如何排序?
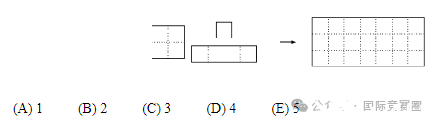
A 3 7 rectangle is covered without overlap by 3 shapes of tiles: 2 2, 1 4, and 1 1, shown below.
What is the minimum possible number of 1 1 tiles used?
一个3x7的矩形被无重叠地覆盖了3种形状的瓷砖:2x2、1x4和1x1。如下图所示。使用的1x1瓷砖的最少可能数量是多少?
On Monday Taye has $2. Every day, he either gains $3 or doubles the amount of money he had on the previous day. How many different dollar amounts could Taye have on Thursday, 3 days later?
在星期一,Taye有2美元。每天,他要么获得3美元,要么将前一天的钱数翻倍。那么在三天后的星期四,Taye可能拥有多少不同的美元总金额?
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
All of the marbles in Maria's collection are red, green, or blue. Maria has half as many red marbles as green marbles and twice as many blue marbles as green marbles. Which of the following could be the total number of marbles in Maria's collection?
玛丽亚收集的弹珠都是红色、绿色或蓝色的。玛丽亚拥有的红色弹珠数量是绿色弹珠的一半,拥有的蓝色弹珠数量是绿色弹珠的两倍。下面哪个可能是玛丽亚收集的弹珠总数?
(A) 24 (B) 25 (C) 26 (D) 27 (E) 28
In January 1980 the Mauna Loa Observatory recorded carbon dioxide (CO2) levels of 338 ppm (parts per million). Over the years the average CO2 reading has increased by about 1.515 ppm each year. What is the expected CO2 level in ppm in January 2030? Round your answer to the nearest integer:
1980年1月,莫纳罗亚天文台记录的二氧化碳(CO2)水平为338ppm(百万分之一)。多年来,平均CO2读数每年增加约1.515ppm。2030年1月的预期CO2水平是多少ppm?四舍五入到最接近的整数。
(A) 399 (B) 414 (C) 420 (D) 444 (E) 459
The coordinates of △ABC are A(5, 7), B(11, 7) and C(3, y), with y > 7. The area of △ABC is 12.What is the value of y?
三角形ABC的坐标分别为A(5,7)、B(11,7)和C(3,y),其中y>7。三角形ABC的面积为12,求y的值。
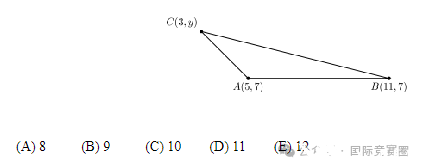
(A) 8 (B) 9 (C) 10 (D) 11 (E) 12
Rohan keeps a total of 90 guppies in 4 fish tanks.
● There is 1 more guppy in the 2nd tank than in the 1st tank.
● There are 2 more guppies in the 3rd tank than in the 2nd tank.
● There are 3 more guppies in the 4th tank than in the 3rd tank.
How many guppies are in the 4th tank?
罗罕总共在4个鱼缸里养了90条孔雀鱼。
-第二个鱼缸里的孔雀鱼比第一个鱼缸里的多1条。
-第三个鱼缸里的孔雀鱼比第二个鱼缸里的多2条。
-第四个鱼缸里的孔雀鱼比第三个鱼缸里的多3条。
第四个鱼缸里有多少条孔雀鱼?
(A)20 (B)21 (C)23 D)24 (E) 26
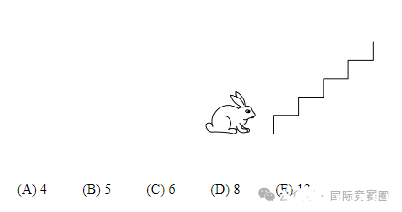
Buzz Bunny is hopping up and down a set of stairs, one step at a time. In how many ways can Buzz
start on the ground, make a sequence of 6 hops, and end up back on the ground? (For example, one
sequence of hops is up-up-down-down-up-down.)
一次只能跳一个台阶,正在上下跳跃。问Buzz有几种方式可以从地面开始,跳跃6次,最终
(A) 20 (B) 21 (C) 23 (D) 24 (E) 26
回到地面?(例如,其中一种跳跃序列是上、上、下、下、上、下。)
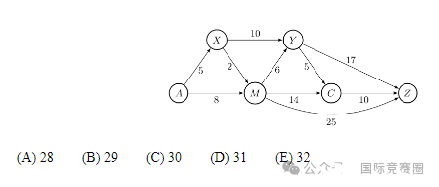
The one-way routes connecting towns A, M, C, X,Y, and Z are shown in the figure below (not
drawn to scale). The distances in kilometers along each route are marked. Traveling along these
routes, what is the shortest distance from A to Z in kilometers?
连接城镇A、M、C、X、Y、Z的单向路线如下图所示(未按比例绘制)。沿每条路线的距
离以公里为单位进行标记。沿着这些路线旅行所有城镇都要去一遍,A到Z之间最短的距离是多少公里?

Minh enters the numbers 1 through 81 into the cells of a 9x 9 grid in some order. She calculates the
product of the numbers in each row and column. What is the least number of rows and columns that
could have a product divisible by 3?
将数字1到81按照某种顺序放入9x9网格的单元格中。她计算每一行和每一列中数字的乘积可被3整除的行数和列数最少为多少?
(A)8
B) 9
(C) 10
(D) 11
E) 12
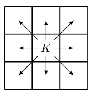
A chess king is said to attack all the squares one step away from it, horizontally, vertically, ordiagonally. For instance, a king on the center square of a 3x3 grid attacks all 8 other squares. as shown below. Suppose a white king and a black king are placed on different squares of a 3x3 grid so that they do not attack each other. In how many ways can this be done?
据说国际象棋的国王可以攻击其横向、纵向或对角线上相隔一步的所有空格。例如,位于3x3网格中心的国王可以攻击其他8个空格,如下所示。假设白王和黑王被放置在3x3网格的不同方格中,并且他们按照箭头方向移动一格也无法碰到对方,它们就不会互相攻击。有多少种方法可以做到这一点?
(A)20 (B)24 (C)27 (D) 28 (E) 32
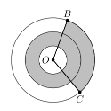
Three concentric circles centered at 0 have radii of 1,2, and 3. Points B and C lie on the largest
circle. The region between the two smaller circles is shaded, as is the portion of the region between
the two larger circles bounded by central angle BOC, as shown in the figure below. Suppose the
shaded and unshaded regions are equal in area. What is the measure of ∠BOC in degrees?
以0为中心的三个同心圆的半径分别为1、2和3。点B和点C在最大的圆上。两个较小的圆之间的区域被着色,两个较大的圆之间BOC角的所夹的被着色的部分,如下图所示。假设着色区域和未着色区域面积相等,则∠BOC的度数是多少?
(A) 108 (B) 120 (C) 135 (D) 144 (E) 150
Jordan owns 15 pairs of sneakers. Three fifths of the pairs are red and the rest are white. Two thirds
of the pairs are high-top and the rest are low-top. The red high-top sneakers make up a fraction of
the collection. What is the least possible value of this fraction?
乔丹有15双运动鞋。五分之三是红色的,其余都是白色的。三分之二是高帮的,其余都是低帮的。红色高帮运动鞋占总数的一小部分。这个分数的最小可能值是多少?
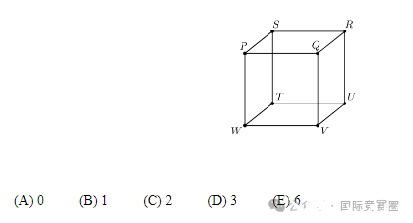
Any three vertices of the cube PQRSTUVW, shown in the figure below, can be connected to form a triangle. (For example, vertices P.Q.and R can be connected to form isosceles△PQR.) How many of these triangles are equilateral and contain P as a vertex?
如下图所示,立方体PQRSTUVW的任意三个顶点都可以连接成一个三角形。(例如,顶点 P、Q和R可以连接成等腰三角形▲POR。)这些三角形中,有多少个是等边三角形并且包含P作为一个顶点?
Problems 21.
A group of frogs (called an army) is living in a tree. A frog turns green when in the shade and turns yellow when in the sun. Initially the ratio of green to yellow frogs was 3 : 1. Then 3 green frogs moved to the sunny side and 5 yellow frogs moved to the shady side. Now the ratio is 4 : 1. What is the difference between the number of green frogs and yellow frogs now?
一组青蛙(称为军队)住在树上。在阴凉处的青蛙会变绿,在阳光下则会变成黄色。最初,绿蛙与黄蛙的比例是3:1。然后三只绿蛙移到阳光明媚的一侧,五只黄蛙移到阴凉处。现在的ratio是4:1。现在绿蛙和黄蛙的数量差是多少?
(A) 10 (B) 12 (C) 16 (D) 20 (E) 24
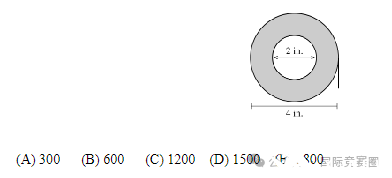
A roll of tape is 4 inches in diameter and is wrapped around a ring that is 2inches in diameter. A cross section of the tape is shown in the figure below. The tape is 0.015 inches thick. If the tape i completely unrolled, approximately how long would it be? Round your answer to the nearest 100 inches.
一卷磁带的直径为4英寸,并缠绕在直径为2英寸的环上。如下图所示是磁带的横截面。磁带的厚度为0.015英寸。如果完全展开磁带,它大约有多长?将答案四舍五入到最接近的100英寸。
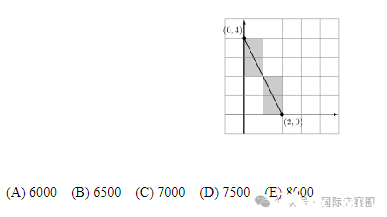
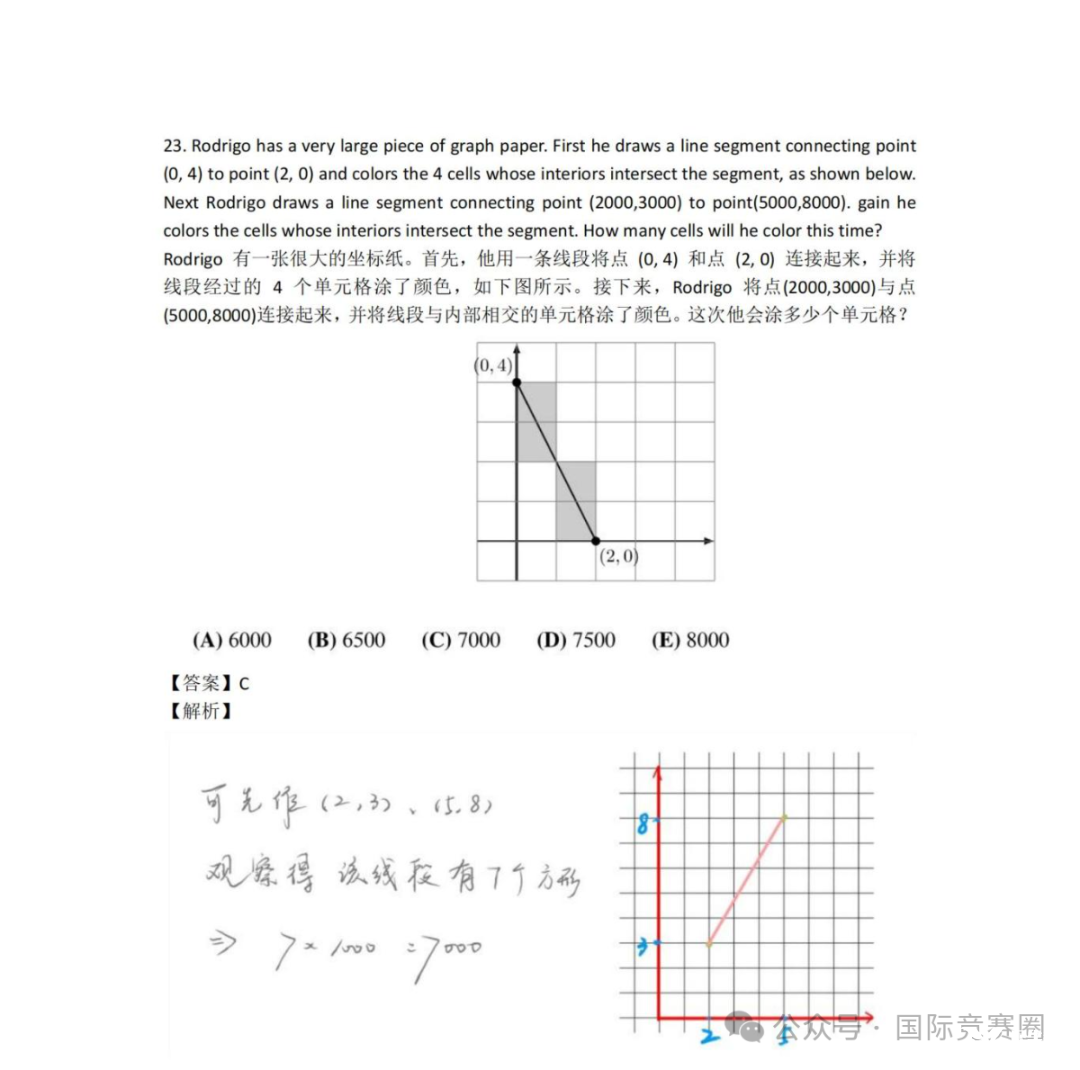
Rodrigo has a very large piece of graph paper. First he draws a line segment connecting point (0,4) to point (2,0) and colors the 4 cells whose interiors intersect the segment, as shown below. Next Rodrigo draws a line segment connecting point (2000,3000) to point (5000, 8000).Again he colors the cells whose interiors intersect the segment. How many cells will he color this time?
有一张很大的坐标纸。首先,他用一条线段将点(0,4)和点(2,0)连接起来,并将线段经过的4个单元格涂了颜色,如下图所示。接下来,Rodrigo将点(2000,3000)与点(5000,8000)连接起来,并将线段与内部相交的单元格涂了颜色。这次他会涂多少个单元格?
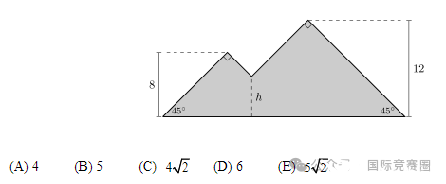
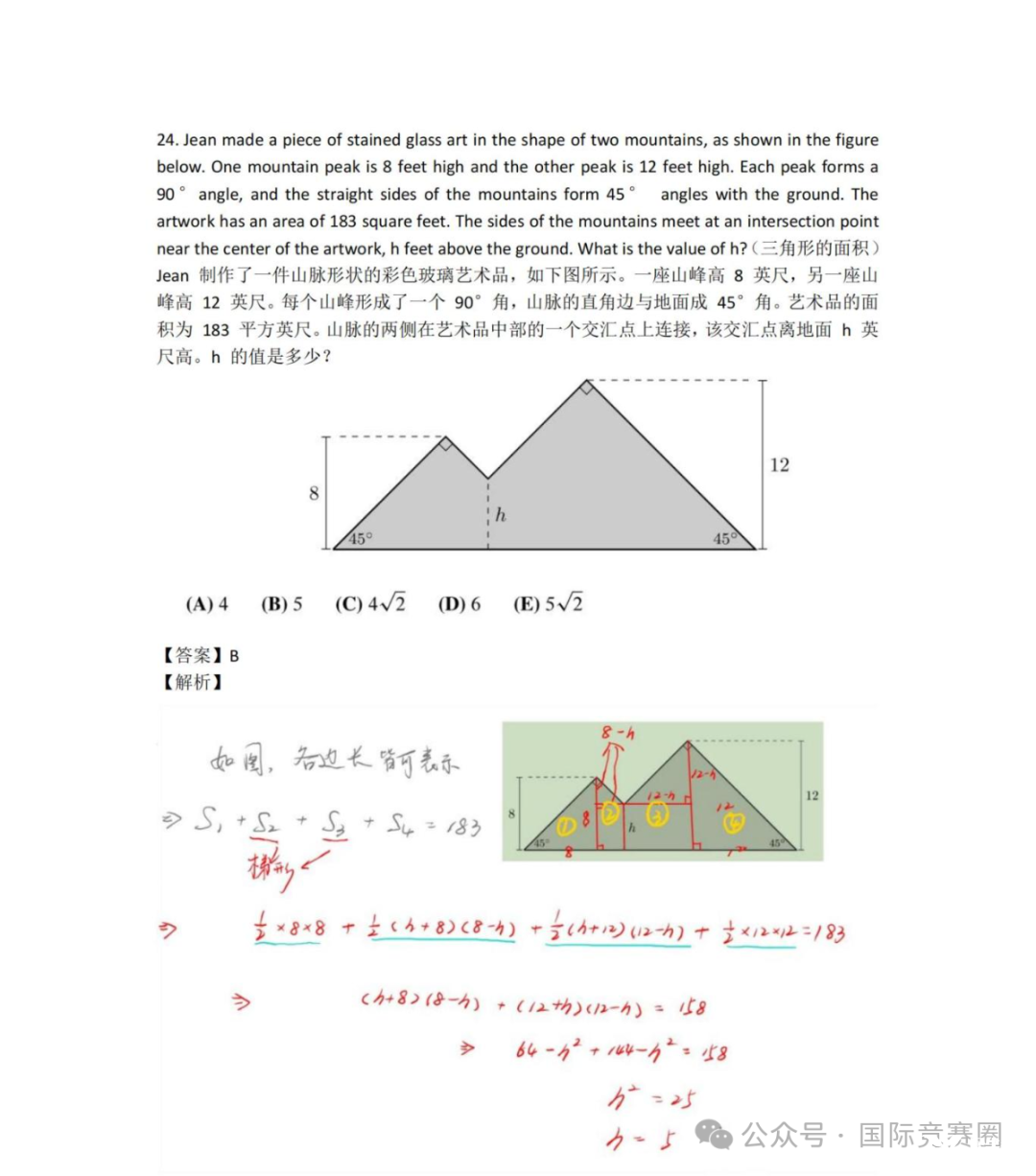
Jean made a piece of stained glass art in the shape of two mountains, as shown in the figure below.
One mountain peak is 8 feet high and the other peak is 12 feet high. Each peak forms a 90°angle,and the straight sides of the mountains form 45° angles with the ground. The artwork has an area of 183 square feet. The sides of the mountains meet at an intersection point near the center of the artwork, h feet above the ground. What is the value of h?
(三角形的面积)Jean制作了一件山脉形状的彩色玻璃艺术品,如下图所示。一座山峰高8英尺,另一座山峰高12英尺。每个山峰形成了一个90°角,山脉的直角边与地面成45°角。艺术品的面积为183平方英尺。山脉的两侧在艺术品中部的一个交汇点上连接,该交汇点离地面h英尺高。h的值是多少?
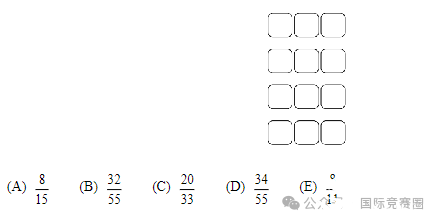
A small airplane has 4 rows of seats with 3 seats in each row. Eight passengers have boarded the plane and are distributed randomly among the seats. A married couple is next to board. What is the probability there will be 2 adjacent seats in the same row for the couple?
一架小型飞机有4排座位,每排有3个座位。8名乘客先登机后随机就坐。然后一对已婚夫妇随后登机。这对夫妇坐在同一排且相邻的概率是多少?
同学们做完真题可以在这里对答案!下面还有更详细的解析哦!
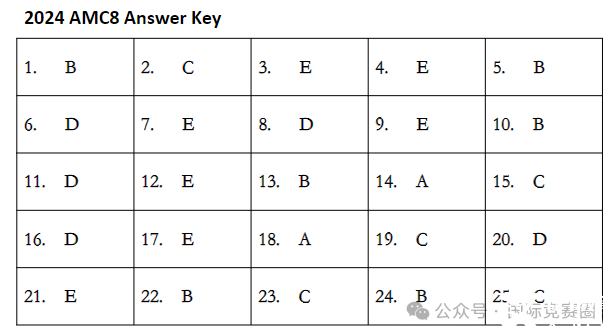
2024AMC8真题解析














还有AMC8历年真题可领取

关注公号扫码领取
犀牛国际针对2025-2026年备考AMC8数学竞赛的同学,开设Pre-AMC8、AMC8基础班,强化班、冲刺班、全程班等多种班型,针对不同年级不同基础的学生,因材施教,确保学员能够学的懂,跟得上。
Pre-AMC8课程主要面向低年级学生,教学内容以小学奥数6大模块以及小学数学重难知识点为主,目标在于帮助低年级段学生拿到AMC8竞赛低龄成就奖。

AMC8课程是Pre-AMC8的进阶课程,要求学生有一定的数学基础,授课内容以AMC8竞赛技巧,AMC8重难点,代数以及高年级知识点为主要内容,目标在于帮助学员更好冲刺前1%和前5%奖项。


AMC04-17


物理碗04-23

物理碗06-05


化学竞赛01-11